Различные подходы к определению понятия функции

- представление о функциональной зависимости переменных величин в реальных процессах и в математике;

- представление о функции как о соответствии;

- построение и использование графиков функций, исследование функций;

- вычисление значений функций, определенных различными способами.

В процессе обучения алгебре все указанные компоненты присутствуют при любом подходе к понятию функции, но акцент может быть сделан на одном из них. Как только что мы отметили, функциональный компонент является основой введения и изучения понятия функции. На этой основе при организации работы над определением вводятся и другие компоненты, проявляющиеся в различных способах задания функциональной зависимости и ее графического представления.

Рассмотрим теперь взаимодействие компонентов на примере, относящемся к формированию прикладных умений и навыков.

Пример 1

. С мороза в комнату внесли банку со льдом и стали наблюдать за изменением температуры вещества в банке: лед постепенно таял, когда он растаял весь, температура воды стала повышаться, пока не сравнялась с температурой в комнате.

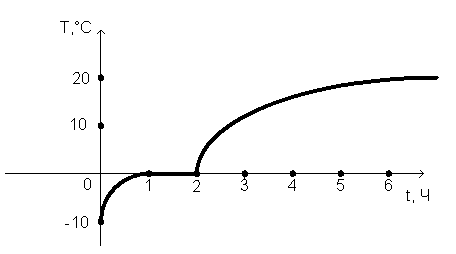
Рис.1.1. График зависимости температуры от времени

Ответьте на вопросы:

а) Какова исходная температура льда?

б) За какое время температура льда повысилась до 0 °С?

в) Какая температура в комнате?

г) Укажите область, на которой определена функция, промежутки ее возрастания, промежуток, на котором она постоянна.

В этом примере необходимо использовать все компоненты, кроме последнего, вычислительного компонента. Процесс с самого начала представлен как функциональная зависимость. В вопросах требуется уточнить характер этой зависимости (вопрос г)), выяснить соответствующие значения функции и аргумента в определенные моменты процесса (вопросы а) и в)).

Понятие функции, в системе формирования которого должны присутствовать такие задания, сразу выступает в курсе математики как определённая математическая модель, что и является мотивировкой для его углублённого изучения.

Новое в образовании:

Психолого-педагогические особенности развития детей старшего дошкольного возраста
Дошкольное детство — большой и ответственный период психического развития ребенка. Это возраст первоначального фактического формирования личности. Как показывают современные исследования, на протяжении дошкольного периода у ребенка не только интенсивно развиваются все психические функции, формируют ...

Результаты опроса по проектированию инновационных процессов в системе ВПО
В данном параграфе мы представляем результаты педагогического эксперимента, в котором проводился мониторинг проектирования в образовательном процессе вузов России инновационных процессов. Анкета № 1 для преподавателей по организации образовательного процесса в вузе приведена в приложении 1. Опрашив ...

Анализ формирования мышления в традиционном преподавании биологии
В современной школе используется три относительно обособленных и отличающихся рядом признаков вида обучения: Объяснительно-иллюстративное, называемое также традиционным, сообщающим или конвенциональным (обычным); Проблемное; Программированное и развившееся на его основе компьютерное обучение. Педаг ...