Роль, функции классификации при формировании понятий

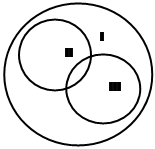Проанализируем получившуюся картину. Круг, изображающий множество N натуральных чисел, разбился на 4 непересекающиеся области – они пронумерованы римскими цифрами. Каждая область изображает некоторое подмножество множества N . Определим, какие числа оказались в каждом из этих непересекающихся подмножеств. Подмножество I состоит из чисел, кратных 3 и 5; подмножество II – из чисел, кратных 3 и не кратным 5; подмножество III – из чисел, кратных 5 и не кратных 3; подмножество IV – из чисел, не кратных 3 и не кратных 5. Объединение этих четырех подмножеств есть множество N.

Для формирования умений по классификации и систематизации целесообразно на практических занятиях (или в качестве самостоятельной работы) предлагать упражнения на составление классификационных схем. Порядок составления таких схем предполагает схематическое изображение изученных в данной теме понятий на основе их родо - видовых отношений.

Классификационные схемы целесообразно составлять в конце изучения темы или раздела.

При изложении математики в школе часто приходится прибегать к классификации. В процессе классификации образуется система изучаемых понятий. Полезны классификации при повторении, так как при этом систематизируется изучаемый материал, ученики получают более полное представление о взаимосвязях между понятиями и о системе математических понятий. В процессе этой работы важно широко использовать таблицы, схемы, диаграммы, иллюстрирующие вопросы классификации и их применение при решении задач.

Применение приема классификация на уроках позволяет существенно расширить имеющиеся в практике приемы работы, способствуют формированию положительных мотивов в учебной деятельности, так как подобная работа содержит и элементы игры и элементы поисковой деятельности, что в свою очередь повышает активность учащихся и обеспечивает самостоятельное выполнение работ.

Новое в образовании:

Понятие умственной отсталости
Для успешной коррекции нарушении необходимо точно понимать, каких детей следует считать умственно отсталыми, в чем особенность их познавательной и эмоционально-волевой сферы. «Исследования ученных (Л.В. Выготский, А.Р. Лурия, К.С. Лебединский, В.И. Лубовский, М.С. Певзнер, Г.Е. Сухарева и др.) дают ...

Направления, формы и методы этнокультурно коннотированного дополнительного образования художественно-эстетической направленности
Опытно-экспериментальная работа по реализации процесса воспитания эстетической культуры школьников осуществлялась на базе Элистинского Дворца детского творчества Республики Калмыкия. В процессе констатирующего эксперимента решались следующие задачи: 1. Зафиксировать достигнутый уровень жизнедеятель ...

Психолого-педагогическая характеристика детей с общим недоразвитием речи
Под общим недоразвитием речи у детей с нормальным слухом и первично сохранным интеллектом следует понимать такую форму речевой аномалии, при которой нарушается формирование каждого из компонентов речевой системы: фонетики, лексики, грамматики. При этом отмечается нарушение как смысловой, так и прои ...