Роль, функции классификации при формировании понятий

Существуют различные способы проведения классификации:

Классификация по видоизмененному признаку. Элементы понятия, подлежащего классификации, обладают несколькими признаками. В качестве основания классификации могут использоваться различные признаки классифицируемого понятия.

Пример: ученики третьего класса легко могут разбить множество Х треугольников на три класса: остроугольные, прямоугольные и тупоугольные. Действительно, выделенные подмножества попарно не пересекаются (среди остроугольных нет прямоугольных и тупоугольных, среди прямоугольных – тупоугольных) и их объединение совпадает с множеством Х. Однако то, что не всякая система подмножеств данного множества представляет собой разбиение этого множества им понять сложно. Например, если из множества Х треугольников выделить подмножества равнобедренных, равносторонних и разносторонний, то разбиения множества Х на классы мы не получим, поскольку множества равнобедренных и равносторонних треугольников пересекаются (все равносторонние треугольники являются равнобедренными).

Из таблицы видно, что образовалось девять классов, из которых некоторые пусты (см. табл.1.1 ).

В случае алгебраических уравнений при одновременном использовании двух оснований классификаций получаем, например, класс уравнений первой степени с двумя переменными или класс уравнений второй степени с одной переменной и т. д. При одновременной классификации натуральных чисел по признаку делимости их на 2 и на 3 получаем класс натуральных чисел, делящихся на 6, и др.

Выбор признака классификации зависит от целей классификации, от практических задач. Важнейшим требованием к признаку (основанию) классификации является его объективность. Нельзя делить книги на интересные и неинтересные, задачи на легкие и трудные, так как такие признаки носят субъективный характер. В самом деле, одни и те же теоремы могут быть легкими для одних учеников и трудными для других.

2) Дихотомическая (от греческих слов dicha и tome «сечение на две части») классификация представляет собой деление объема классифицируемого понятия на два видовых понятия, один из которых обладает данным признаком, а другой не обладает им.

Сравнивая дихотомическую классификацию с классификацией по видоизмененному основанию, можно выделить ряд преимуществ. Эта классификация всегда удовлетворяет требованию соразмерности, так как объединение образованных классов полностью исчерпывает объем понятия, подлежащего классификации. Кроме того, образованные классы всегда исключают друг друга.

Однако дихотомическая классификация не лишена недостатков. Так, разделив объем понятий на два противоречащих друг другу видовых понятия, мы оставляем весьма неопределенным то видовое понятие, которое содержит частицу «не». Например, разделив класс тригонометрических уравнений на простейшие уравнения и не простейшие, оставляем достаточно неясным объем класса не простейших тригонометрических уравнений.

Пример. Применяя дихотомию можно провести классификацию треугольников и четырехугольников так:

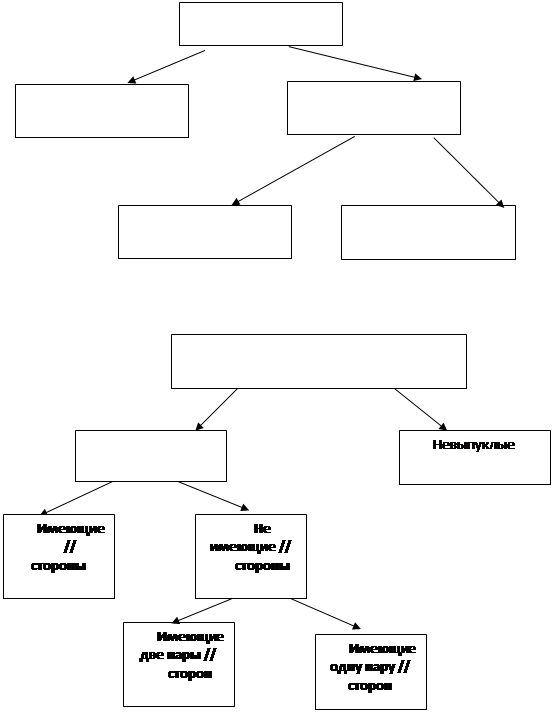Дихотомия часто используется при разбиении данного множества одновременно по нескольким основаниям.

3) Дихотомия по разным основаниям – разбиение объема классифицируемого понятия по независимым основаниям на 2п класса.

Имеет место следующая теорема: при разбиении множества М по n независимым основаниям образуется 2 n класса (n ).

Эта теорема о разбиении множества по n независимым основаниям может быть использована для решения задач определенного типа.

Для решения таких задач целесообразно использовать наглядную интерпретацию разбиения множества на классы с помощью диаграмм Эйлера - Венна. В диаграмме заполняется числом элементов каждая ее часть (класс) в соответствии с условиями задачи, что и ведет к решению задачи.

Пример. Рассмотрим два свойства натуральных чисел: «быть кратным 3» и «быть кратным 5».При помощи этих свойств из множества натуральных чисел можно выделить два подмножества: А - подмножество чисел, кратных 3, и В – подмножество чисел, кратных 5. Эти подмножества пересекаются, но ни одно из них не является подмножеством другого.

Новое в образовании:

Реализация системного подхода в работе педагога дополнительного образования детей
Многочисленные наблюдения показывают, что эффективность профессиональной деятельности педагога дополнительного образования во многом предопределена его умением на системно-целевой основе ставить и решать многочисленные задачи воспитания и обучения учащихся. Системное видение своей профессиональной ...

Содержание физического воспитания детей 3—7 лет
Физическое воспитание детей дошкольного возраста осуществляется в соответствии с «Программой воспитания в детском саду». 3адачи физического воспитания многообразны. Они тесно связаны между собой, с музыкальным, эстетическим воспитанием, развитием речи и т. д. Одна из задач заключается в совершенств ...

Возрастные и индивидуальные особенности ребенка
Личностное развитие человека несет на себе печать его возрастных и индивидуальных особенностей, которые необходимо учитывать в процессе воспитания. С возрастом связан характер деятельности человека, особенности его мышления, круг его запросов, интересов, а также социальные проявления. Вместе с тем ...