Суть метода координат

Немного из истории координатного метода.

В настоящее время уже очень большое число специалистов из разных областей науки имеют представление о прямоугольных декартовых координатах на плоскости, так как эти координаты дают возможность наглядно при помощи графика изобразить зависимость одной величины от другой. Название «декартовы координаты» наводит на ложную мысль о том, что эти координаты были открыты Декартом. В действительности прямоугольные координаты использовались в геометрии еще до нашей эры. Древний математик александрийской школы Аполлоний Пергский (живший в III-II веке до н. э.) уже фактически пользовался прямоугольными координатами. Он определял и изучал с их помощью хорошо известные в то время кривые: параболу, гиперболу и эллипс.

Аполлоний задавал их уравнениями: у2 =рх (парабола)

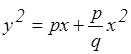(гипербола)

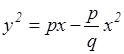(эллипс, где р и q положительны)

Он, конечно, не выписывал уравнения в этой геометрической форме, так как в те времена не существовало еще алгебраической символики, а описывал уравнения, пользуясь геометрическими понятиями; у2 в его терминологии есть площадь квадрата со стороной у; рх - площадь прямоугольника со сторонами р и х и т.д. С этими уравнениями связаны названия кривых. Парабола по-гречески обозначает равенство: квадрат имеет площадь у2 равную площади рх прямоугольника. Гипербола по-гречески обозначает избыток: площадь квадрата у2 превосходит площадь рх прямоугольника. Эллипс по-гречески обозначает недостаток: площадь квадрата меньше площади прямоугольника.

Декарт внес в прямоугольные координаты очень важное усовершенствование, введя правила выбора знаков. Но главное, пользуясь прямоугольными координатами, он построил аналитическую геометрию на плоскости, связав этим геометрию и алгебру. Нужно сказать, однако, что одновременно с Декартом построил аналитическую геометрию и другой французский математик, Ферма.

Значение аналитической геометрии состоит, прежде всего, в том, что она установила тесную связь между геометрией и алгеброй. Эти две ветви математики ко времени Декарта достигли уже высокой степени совершенства. Но развитие их в течение тысячелетий шло независимо друг от друга, и ко времени появления аналитической геометрии между ними намечалась лишь довольно слабая связь.

Координаты позволяют определять с помощью чисел положение любой точки пространства или плоскости. Это дает возможность «шифровать» различного рода фигуры, записывая их при помощи чисел. Соотношения между координатами чаще всего определяет не одну точку, а некоторое множество (совокупность) точек. Например, если отметить все точки, у которых абсцисса равна ординате, т. е. точки, координаты которых удовлетворяют уравнению х=у, то получится прямая линия - биссектрисы первого и третьего координатных углов.

Иногда, вместо «множество точек», говорят «геометрическое место точек». Например, геометрическое место точек, координаты которых удовлетворяют соотношению х=у - это, как было сказано выше, биссектрисы первого и третьего координатного угла. Установление связей между алгеброй, с одной стороны, и геометрией - с другой, было по существу, революцией в математике. Оно восстановило математику как единую науку, в которой нет «китайской стены» между отдельными ее частями.

Суть метода координат

Сущность метода координат как метода решения задач состоит в том, что, задавая фигуры уравнениями и выражая в координатах различные геометрические соотношения, мы можем решать геометрическую задачу средствами алгебры. Обратно, пользуясь координатами, можно истолковывать алгебраические и аналитические соотношения и факты геометрически и таким образом применять геометрию к решению алгебраических задач.

Новое в образовании:

Современные подходы к решению проблемы информационной безопасности школьника
С развитием информационно-коммуникативных технологий в системе образования все больше используется опыт, накопленный сетевыми сообществами в обучении и приобщении учителей и школьников к участию в жизни таких сообществ, существующих на базе сетевых центров науки, искусства, здравоохранения, професс ...

Исследование состояния связной описательной речи детей старшего дошкольного возраста с общим речевым недоразвитием описательной речи
При подготовке детей к школьному обучению большое значение приобретает формирование и развитие монологической речи как важнейшего условия полно­ценного усвоения знаний, развитие логического мышления, творческих способно­стей и других сторон психической деятельности. Особое внимание в формировании с ...

Методические рекомендации по формированию краеведческих знаний младших школьников с ЗПР во внеклассной работе
Результаты обучающего эксперимента были учтены при разработке методических рекомендаций по повышению эффективности формирования краеведческих знаний младших школьников с ЗПР. 1.В настоящее время действующие в специальных (коррекционных) школах VII вида программы строятся по принципу сочетания трех ...