Речь как средство общения и один из ведущих показателей уровня сформированности коммуникативной компетентности

Математика имеет огромные возможности для развития мышления и логически совершенной речи. Чтобы рассуждать, провести доказательство теоремы или самостоятельно решить задачу, нужно не просто заучить материал, а самостоятельно размышлять. Ученик, не разобравшись в идее доказательства, обязательно при ответе допустит ту или иную неточность; для правильного ответа он должен понять систему рассуждений, ту мысль, которая положена в их основу. Ученик должен показать в своем ответе не столько умение запоминания, сколько умение рассуждения.

В математической речи не должно быть слов, не несущих смысловой нагрузки. Лишние слова и предложения могут быть сказаны для оказания эмоционального воздействия на собеседника, для выяснения связей с практическими задачами или с другими научными дисциплинами.

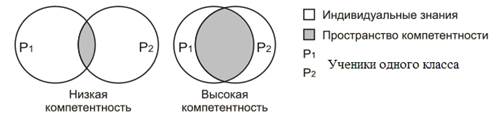
Рис. 1. Соотношение индивидуальных знаний и компетентности

На рис. 1 показано соотношение между индивидуальными знаниями и компетентностью. Здесь пространство компетентности – это требования, которым должен соответствовать любой ученик. Чем больше точек пересечения, тем эффективнее взаимодействие. Не может отдельно взятый человек быть компетентным сам по себе, он всегда компетентен относительно конкретной системы с ее требованиями.

Чтобы научиться применять индивидуальные знания, нужно развивать свою речь. А для этого необходимо:

Определить собственную линию естественно-речевого общения и придерживаться ее как эталона (полная ясность; научность (точное употребление терминов, точность формулировок, определений и предложений, логическая обоснованность рассуждений); соблюдение правил этимологии и синтаксиса (правильное употребление падежей, согласование, употребление союзов, сокращение предложений); литературность (приближение к литературному стилю, живость, образность изложения)).

Уделить особое внимание математической фразеологии и настойчиво обогащать ею научный стиль речи ученика.

Обеспечить правильное употребление учащимися математических терминов, обозначающих понятия, (изучение должно включать: происхождение, буквальный смысл, научный смысл, приведены иллюстрации и примеры). Недостаточно глубокое, поверхностное усвоение понятия является причиной его неправильного употребления учащимися; неясное, неполное понимание термина немедленно влечет за собой неточную, расплывчатую, туманную речь.

Обратить внимание учащихся на выражения и формулировки учебника, разъяснить, что является существенным, определяющим (не упоминание может свести эти формулировки до уровня бессодержательных предложений).

Подчинить речь учащегося тем общим законам, которые учащиеся изучали на уроках русского языка.

Использовать для развития языка письменную речь. Отмечать стилистические, орфографические и в особенности пунктуационные ошибки и делать их объектом активного обсуждения в классе. Эти обсуждения будут каждый раз напоминать учащимся о том, что к недочетам письменных работ относятся не только математические ошибки, но и стилистические, орфографические и пунктуационные недостатки их письменной речи.

Особенно большое значение имеет составление учащимися объяснений к решениям текстовых задач. Они должны быть написаны вполне грамотным и притом непременно связным языком. Речевые ошибки в математических выражениях, допущенные в ранний период обучения, укореняются, если игнорируются недочеты в речи, исходя из соображений, что школьники понимают, о чем идет речь, и просто оговариваются.

Но не только математика может сформировать компетенцию более высокого уровня. Межпредметная интеграция также позволяет укрепить компетенцию. Рассмотрим пример общепредметных компетенций.

Таблица 1. Общепредметные компетенции

Новое в образовании:

Организация и проведение опытно-экспериментальной работы по формированию экологической культуры младших школьников посредством дидактических игр
ІІ этап (октябрь 2012 – февраль 2013г.) – формирующий эксперимент. Цель формирующего эксперимента – организовать и провести экспериментальную работу по формированию экологической культуры младших школьников с помощью специально разработанного комплекса дидактических игр. В данном параграфе представ ...

Структура педагогической деятельности
Прежде, чем приступить к рассмотрению сущности педагогических инноваций, методов их выявления и изучения, необходимо проанализировать структуру педагогической деятельности и определить, какое место занимает в ней инновационная деятельность учителя. Современные исследования Н.В. Кузьмина, В.А. Сласт ...

Трудности формирования навыков самообслуживания у детей из неблагополучных семей
Неблагополучная семья – это семья, в которой ребенок испытывает дискомфорт, стресс, пренебрежение со стороны взрослых, подвергается насилию или жестокому обращению. Главной характеристикой такой семьи является отсутствие любви к ребенку, заботы о нем, удовлетворения его нужд, защиты его прав и зако ...