Методика изучения линейной, квадратной и кубической функции в VII классе

Пример 6.

Задан график функции у=х2. Построить на этом чертеже график функции у=х2+1.

Заметим, что при заданном значении аргумента хо (рассматриваются, конечно, конкретные значения) значения функции у=х2+1 на одно и то же число, равное 1, больше значений функции у=х2. Поэтому для построения соответствующей точки на графике второй функции достаточно поднять на 1 точку графика первой функции с абсциссой Хо. Следовательно, чтобы построить весь график второй функции, нужно поднять на 1 график первой.

Это рассуждение хорошо усваивается учащимися, целесообразно применить его и при изучении класса линейных функций. В дальнейшем при обобщении свойств графиков его можно сформулировать так: «Чтобы построить график функции у=f(x)+с по известному графику функции у=f(х), можно произвести параллельный перенос второго графика на с единиц вдоль оси ординат».

После этой подготовки, казалось бы, можно приступить к изучению графиков произвольных квадратичных функций. Но здесь возникает трудность: коэффициент при первой степени неизвестного не имеет для квадратичной функции у=ах2+bх+с достаточно простого геометрического смысла. Именно поэтому приходится идти обходным путем, следуя тем же преобразованиям, которые производились при выводе формулы решения квадратного уравнения, и вводить в рассмотрение новый подкласс квадратичных функций вида у=а(х-b)2. Объяснения при построении графиков здесь в целом могут быть такими же, как при рассмотрении функций вида у=x2+с, однако усваивается предлагаемый способ здесь с большим трудом, поэтому требуется достаточное количество упражнений для закрепления. После таких приготовлений построение графика, а также изучение его свойств происходят без принципиальных затруднений.

Отметим здесь один частный, но полезный прием, который состоит в использовании системы заданий, имеющих цель — дать представление о тех или иных чертах данной функции или целого класса без указания точного значения величин, связанных с рассматриваемым вопросом. Этот прием можно назвать качественным или оценочным исследованием функции. Приведем два примера, связанные с изучением квадратичных функций.

Пример 7.

На рисунке изображены графики функций у=х2 и у= —0,5х2. Как относительна них пройдет график функции y=0,5х2; -2х2; Зх2? Это задание не предполагает «точного» построения искомого графика; достаточно лишь указание на область, где он расположен, или его эскизное построение.

Пример 8.

На рисунке изображен график функции у=х2+1, пользуясь этим чертежом, изобразить от руки график функции у=х2+ 0,3. Проверить правильность сделанного эскиза: вычислить значения функции у = х2 при х=±0,5; ±1,5 и отметить точки графика. Каким преобразованием можно перевести график функции

у=х2-1 в график функции у=х2?

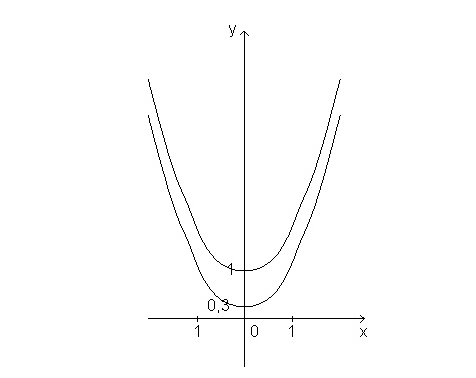
Рис.2.3. График функции у=х2+1

Цель задания — согласовать зрительный образ графика, его геометрические свойства и формулу. График функции у = x2 + 0,3 симметричен относительно оси ординат, значит, рисунок не должен быть скошенным. Его симметричность подчеркивается симметричным расположением «пробных» значений аргумента. Положение точек на чертеже должно выправить распространенную неточность в изображении графиков квадратичных функций: нарисованные от руки ветви параболы, как правило, расположены гораздо шире, чем должны быть. Поэтому пробные точки (их ординаты вычисляются по условию, а не ищутся по чертежу) попадают в полосу между изображенными линиями. То, что графики сближаются по мере удаления от начала координат, требует пояснений, которые можно сделать при обсуждении.

К изучению класса кубических функций привлекается прием, аналогичный изучению квадратичных функций, основанный на использовании геометрических преобразований для построения графика произвольной кубической функции из кубической параболы стандартного положения — графика функции у=ах3, а≠0.

Новое в образовании:

Классификация детских площадок по компоновочной структуре
Единый игровой комплекс (В таком комплексе дизайнеры стремятся собрать воедино разнообразные игровые элементы, объединенные общим стилистическим решением. Создатели таких комплексов стремятся к колористическому единству и повторяемости основных декоративных элементов, наличию общей идеи. При этом п ...

Содержание физического воспитания детей 3—7 лет
Физическое воспитание детей дошкольного возраста осуществляется в соответствии с «Программой воспитания в детском саду». 3адачи физического воспитания многообразны. Они тесно связаны между собой, с музыкальным, эстетическим воспитанием, развитием речи и т. д. Одна из задач заключается в совершенств ...

Генезис концептуальных основ физического воспитания
В апреле 2000 года на совместной Коллегии Министерства образования Республики Беларусь и Министерства спорта и туризма Республики Беларусь была обсуждена и одобрена Концепция физического воспитания в условиях реформирования системы образования Республики Беларусь. Сформулированные в Концепции предс ...