Методика изучения линейной, квадратной и кубической функции в VII классе

Как и в случае с квадратичной функцией у=х2 видим , что характер изменения значений функции у=х3 неравномерный: на одних участках она растет быстрее, на других — медленнее. Эта особенность выявляется при построении графика, причем целесообразно рассмотреть два графика: один — в крупном масштабе на промежутке,. -1≤x≤1, другой—в мелком масштабе на промежутке, например, -2≤х≤2. Построение можно вести описанным выше методом загущения. Важно отметить свойство кубической параболы - симметричность её графика относительно начала координат.

Далее вводится более широкий класс функций, имеющий вид у=ах3+с. И здесь также коэффициент с получает ясную геометрическую интерпретацию, подойти к которой можно либо явно используя понятие параллельного переноса вдоль оси ординат, либо независимым рассуждением.

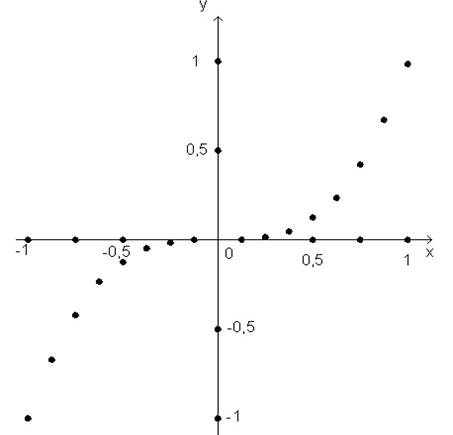
Рис.2.4.

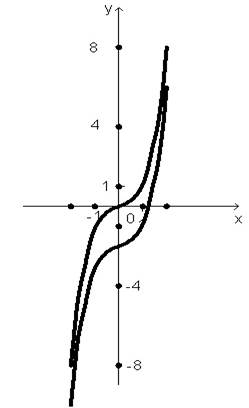
Рис.2.5.

Пример 9.

Задан график функции у=х3. Построить на этом чертеже график функции у=х3-2.

Здесь также можно поступить по аналогии с рассмотренными примерами при рассмотрении квадратичной функции.

Далее необходимо подвести учащихся к основным свойствам функции y=x3:

Область определения - вся числовая прямая;

y=x3 -нечетная функция;

Функция возрастает на всей числовой прямой.

Новое в образовании:

Слово учителя как метод преподавания
Слово учителя – особенное, аудиовизуальное (словесно-образное) средство реализации принципа динамического баланса, действенное средство развития творческих способностей учащихся, в системе познавательных и эмоционально-оценочных компонентов учебно-воспитательного процесса. Слово учителя, особенное ...

Особенности нарушений речи у детей с задержкой психического развития
У детей с ЗПР отмечается замедленный темп речевого развития и большая распространённость нарушения речи. У детей с ЗПР имеют место все нарушения речи, наблюдающиеся у детей с нормальным интеллектом. Наиболее распространённым является нарушения звукопроизношения и нарушения письменной речи (дислекси ...

Психология половых различий
Общеизвестно, что половой диморфизм относится к числу фундаменталь­ных, постоянных характеристик человеческого онтогенеза, а половое разделение труда в той или иной форме существует в любом человече­ском обществе. Проблема соотношения и изменения традиционных сти­лей жизни и психических свойств муж ...