Анализ учебников
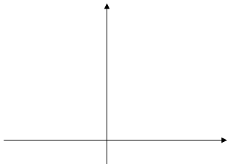
При любом х≠0 значения функции у=2х² больше соответствующего значения функции у=х² в 2 раза. Если переместить каждую точку графика функции у=х² вверх так, чтобы расстояние от точки до оси х увеличилось в 2 раза, то она перейдет в точку графика функции у= 2х², при этом каждая точка графика может быть получена из некоторой точки графика функции у=х². То есть, график функции у=2х² можно получить из параболы у=х² растяжением от оси х в 2 раза (рис.1).
Построим график функции у=![]() х² по таблице значений:
х² по таблице значений:
|
х |
-4 |
-2 |
-1 |
0 |
1 |
2 |
4 |
|
у |
8 |
2 |
-0,5 |
0 |
0,5 |
2 |
8 |
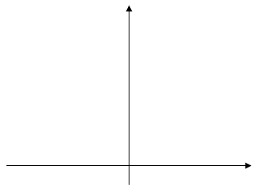
При любом х≠0 значение функций у= ![]() х² меньше соответствующего значения функции у= х² в 2 раза.
х² меньше соответствующего значения функции у= х² в 2 раза.
Рассуждая аналогично предыдущему преобразованию авторы приходят к выводу, что график функции у= ![]() х² можно получить из параболы у= х² сжатием к оси х в 2 раза.
х² можно получить из параболы у= х² сжатием к оси х в 2 раза.
Вообще график функции у=ах² можно получить из параболы у= х² растяжением от оси х в а раз, если а>1, и сжатием к оси х в ![]() раз, если 0<а<1.
раз, если 0<а<1.
Симметрия относительно оси х рассматривается на примере сравнения графиков функций у= ![]() х² и у= -
х² и у= -![]() х².
х².
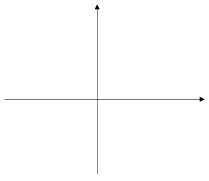
При любом х значение этих функций являются противоположными числами. Значит, соответствующие точки графиков симметричны относительно оси х. То есть, график функции у=-![]() х² может быть получен из графика функции у=
х² может быть получен из графика функции у=![]() х² с помощью симметрии относительно оси х.
х² с помощью симметрии относительно оси х.
Вообще графики функций у=ах² и у=-ах² (при а≠0) симметричны относительно оси х.
В конце каждого пункта авторы предлагают выводы:
-график функции у= -f(х) можно получить из графика функции у= -f(х) с помощью симметрии относительно оси х;
-график функции у= аf(х) можно получить из графика функции у= f(х) с помощью растяжения от оси х в а раз, если а>1, и с помощью сжатия к оси х в ![]() раз, если 0<a<1.
раз, если 0<a<1.
Новое в образовании:
Игры, направленные на развитие памяти и внимания
«Вызови по имени». Дети, предварительно разбившись на две команды, бегают, прыгают в произвольном порядке. Внезапно ведущий подбрасывает мяч и называет имя участника первой команды, который должен поймать мяч. Затем аналогично вызывается участник второй команды. Побеждает команда, поймавшая мяч бол ...
Описание курса 9 класса «Общие закономерности развития»
Программа предназначена для изучения предмета «Общая биология» в 9 классах общеобразовательных учреждений, а также лицеев и гимназий. Программа курса включает в себя полностью вопросы программы общеобразовательной школы 10-11 классов. В ней сохранены все разделы и темы, изучаемые в общеобразователь ...
Причины неудач в организации групповой работы младших
школьников и их устранение
Учителя, пытающиеся использовать на своих уроках групповую работу, поначалу сталкиваются с многочисленными проблемами. Неудачная работа учебных групп в большинстве случаев связана либо с нежеланием, либо с неумением школьников работать вместе. Их необходимо обучить навыкам совместной работы. Внутре ...
НАВИГАЦИЯ
- Главная
- Работа социального педагога с семьей
- Традиционные основы народной педагогики
- Процесс обучения как целостное явление
- Индивидуальный подход в воспитании детей
- Детские игровые площадки
- Особенности учебного процесса в высшей школе
- Педагогика и воспитание
