Система упражнений

На основе анализа учебников мы предлагаем систему упражнений для успешного овладения учащимися умений преобразований графиков функций.

3.1 Симметрия относительно оси абсцисс

№1. Постройте в одной системе координат графики заданных функций и сделайте выводы о взаимном расположении построенных графиков:

а) у= х² и у= -х²; д) у= и у= -; и) у= и у= -;

в) у= 4х² и у= -4х²; е) у= и у= -; к) у= 5 и у= -5;

б) у= х² и у= -х²; ж) у= - и у= ; л) у= - и у= ;

г) у= х² и у= -2х²; з) у= и у= -; м) у= 0,5 и у= -3,5.

№2. Не выполняя построения графиков функций, ответьте на вопрос, как расположен в одной системе координат и по отношению друг к другу графики функций:

а) у= 365х² и у= -365х²; в) у= - и у= ; д) у= и у= -;

б) у=-2,725х² и у=2,725х²; г) у= и у=-; е) у=-523√х и у=523√х.

№3. Задайте число к так, чтобы график функции

1) у= кх² был расположен: 2) у= был расположен: 3) у= к был расположен:

а) в I и III четвертях; а) в I и III четвертях; а) в I четверти;

б) в III и IV четвертях. б) во II и IV четвертях. б) в IV четверти.

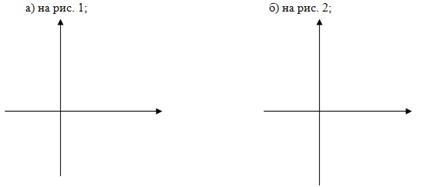
№4. Напишите уравнение параболы у=кх², график которой изображен:

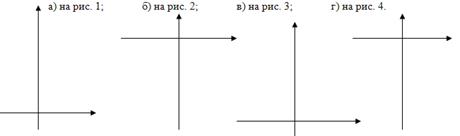
№5. Напишите уравнение гиперболы у=, график которой изображен:

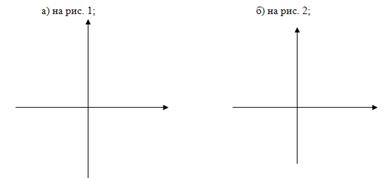
№6. Напишите уравнение функции у=к, график которой изображен:

№7. Постройте график функции симметричный следующим функциям; запишите ее формулу.

а) у= 6х²; в) у= 7х²; д) у= -; ж) у= -; и) у= 1,5;

б) у= -х²; г) у= ; е) у= -; з) у= -4; к) у= -

Новое в образовании:

Развитие взаимодействия дошкольников со сверстниками в условиях образовательного процесса
Дошкольники в условиях дошкольного учреждения взаимодействуют в разных видах деятельности: в игре, на занятиях, в быту и труде. Сюжетно-ролевая игра играет ведущую роль в формировании положительных взаимоотношений детей и формировании положительных морально-нравственных качеств личности старшего до ...

Проблемы правового регулирования воспитательной работы с осужденными к лишению свободы
Согласно ст. 9 УИК воспитательная работа рассматривается в качестве одного из основных средств исправления осужденных. Она призвана сформировать у них уважительное отношение к человеку, обществу, труду, нормам и традициям человеческого общежития, повысить их образовательный и культурный уровень. По ...

Контроль знаний учащихся по биологии: требования, формы, значение
Систематический контроль знаний и умений учащихся - важная составная часть обучения. Методы контроля или проверки знаний и умений тесно связаны с методами всех остальных звеньев учебно-воспитательного процесса: методами изложения учебного материала, закрепления и повторения, обобщения и систематиза ...