Система упражнений

в) = 4+х; е)= 2х-2; и) = ; м) (х+1)² = - .

№13. Решите графически систему уравнений.

а) у= -(х+2)² б) у= -(х-3)² в) у= -х² г) у= д) у=

у= х+1 у= х-6 у= -3х у= (х-3)² у=-2х+2.

№14. Дана функция у=f(x), где:

1) f(x)= , если –3≤х≤3; 2) f(x)= , если –3≤х≤1;

2(х-2)², если 1<х≤3. 2(х-1)², если 1<х≤2.

а) найдите : f(-1); f(2); f(6); а) найдите : f(-3); f(1); f(1,5);

б) постройте график функции у= f(x); б) постройте график функции у= f(x);

в) перечислите свойства функции. в) перечислите свойства функции.

3.3 Параллельный перенос вдоль оси ординат

№1. Постройте в одной системе координат графики функций:

а) у= х² и у= х²+5; д) у= -3 и у= -3+5; и) у= - и у= --1;

б) у= -х² и у= -х²-4; е) у= и у= -4; к) у= и у= +3;

в) у= х² и у= х²-2; ж) у= - и у= --2; л) у= - и у= 5-;

г) у= -3х²+2 и у= -3х²; з) у= и у= +3; м) у= и у= --5.

№2. График, какой функции получится, если параболу у= х² перенести:

а) на 5 единицы масштаба вверх вдоль оси у;

б) на 6 единицы масштаба вниз вдоль оси у;

в) на 1,5 единицы масштаба вверх вдоль оси у;

г) на единицы масштаба вниз вдоль оси у.

№3. График, какой функции получится, если гиперболу у= перенести:

а) на 2 единицы масштаба вверх вдоль оси у;

б) на единицы масштаба вниз вдоль оси у;

в) на 4 единицы масштаба вверх вдоль оси у;

г) на 3,5 единицы масштаба вниз вдоль оси у.

№4. График, какой функции получится, если функцию у= 2,5 перенести:

а) на 3 единицы масштаба вверх вдоль оси у;

б) на 2,5 единицы масштаба вниз вдоль оси у;

в) на 1,2 единицы масштаба вверх вдоль оси у;

г) на 7единиц масштаба вниз вдоль оси у.

№5. Напишите уравнение параболы у= ах²+ m, график которой изображен:

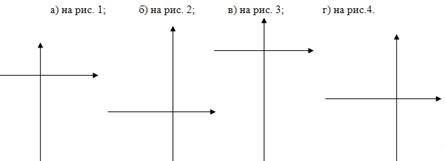
№6. Напишите уравнение гиперболы у= +m, график которой изображен:

Новое в образовании:

Развитие творческих способностей в контексте дополнительного образования
Третья глава исследования содержит в себе материалы, полученные с помощью таких методов сбора информации как анкетирование и экспертное интервью. Исследования были проведены в учреждениях общего и дополнительного образования, и были направлены на рассмотрение проблем, выявленных в теоретической час ...

Результаты опроса по проектированию инновационных процессов в системе ВПО
В данном параграфе мы представляем результаты педагогического эксперимента, в котором проводился мониторинг проектирования в образовательном процессе вузов России инновационных процессов. Анкета № 1 для преподавателей по организации образовательного процесса в вузе приведена в приложении 1. Опрашив ...

Классификация наглядных средств обучения и их виды
Наглядность - "Один из принципов обучения, основанный на показе конкретных предметов, процессов, явлений". На основе непосредственного восприятия предметов или с помощью изображений (наглядности) в процессе обучения у учащихся формируются образные представления и понятия об историческом п ...