Система упражнений

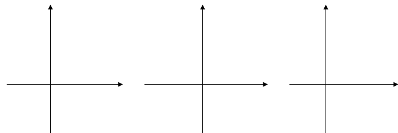
№8. Постройте график функции:

а) у= х², если х≤0; б) у= -2х², если х<0; в) у= 2х², если х≤0;

-х², если х>0. 2х, если х≥0; -х², если х>0.

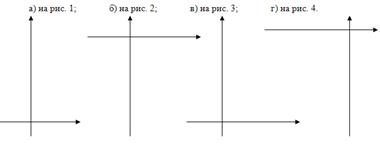
№9. На рисунке изображены графики функций, заданные формулами, соотнесите график и функцию:

у= -х²; у= 4х²; у= -3х²; у= 1,5; у= -2; у= -; у= ; у= ; у= -.

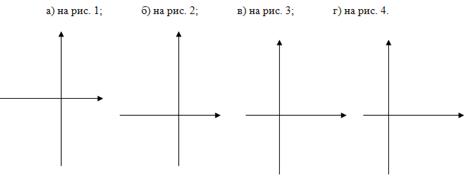
№10. Решите графически уравнение.

а) -х² = 4х-6; в) х² = х+4; д) - = -3х; ж) -= х+5;

б) -2х² = -7х-3; г) х² = -х+4; е) - = 1-х; з) -= -х²

3.2 Параллельный перенос вдоль оси абсцисс

№1. Постройте в одной системе координат графики:

а) у= х² и у= (х+3)²; г) у= и у= ; ж) у= и у= ;

б) у= 2х² и у= 2(х-4)²; д) у= и у= ; з) у=3 и у= 3;

в) у= -х² и у= -(х-2)²; е) у= - и у= -; и) у= - и у= -.

№2. График, какой функции получится, если параболу у= 4х² перенести:

а) на 2 единицы масштаба влево вдоль оси х;

б) на 3 единицы масштаба вправо вдоль оси х;

в) на 6,5 единицы масштаба вправо вдоль оси х;

г) на единицы масштаба влево вдоль оси х.

№3. График, какой функции получится, если гиперболу у= перенести:

а) на 4 единицы масштаба влево вдоль оси х;

б) на единиц масштаба вправо вдоль оси х;

в) на 3.5 единицы масштаба вправо вдоль оси х;

г) на 1 единицу масштаба влево вдоль оси х.

№4. График, какой функции получится, если функцию у= -3 перенести:

а) на 3 единицы масштаба влево вдоль оси х;

б) на единиц масштаба вправо вдоль оси х;

в) на 1,5 единицы масштаба вправо вдоль оси х;

г) на 5 единиц масштаба влево вдоль оси х.

№5. Напишите уравнение параболы у= а(х+l)², график которой изображен:

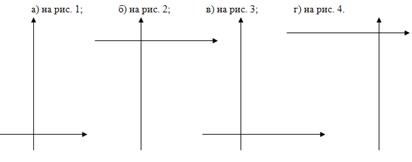
№6. Напишите уравнение гиперболы у= , график которой изображен:

Новое в образовании:

Результаты пробной диагностики функциональной грамотности учащихся г. Караганды
В период февраль-март 2004 года Карагандинским областным институтом повышения квалификации и переподготовки государственных служащих и работников образования была проведена пробная диагностика функциональной грамотности учащихся г. Караганды. За последние 10 лет в нашей республике произошли серьезн ...

Мероприятия по формированию положительных взаимоотношений
На формирующем этапе ставились следующие задачи: 1. Воспитывать дружеские отношения между детьми через совместную деятельность. 2. Вовлечь в совместную деятельность «отверженных» и «непринятых» детей. 3. Развивать умение быть организованными, поддерживать дружеские взаимоотношения со сверстниками. ...

Результаты опроса по проектированию инновационных процессов в системе ВПО
В данном параграфе мы представляем результаты педагогического эксперимента, в котором проводился мониторинг проектирования в образовательном процессе вузов России инновационных процессов. Анкета № 1 для преподавателей по организации образовательного процесса в вузе приведена в приложении 1. Опрашив ...