Система упражнений
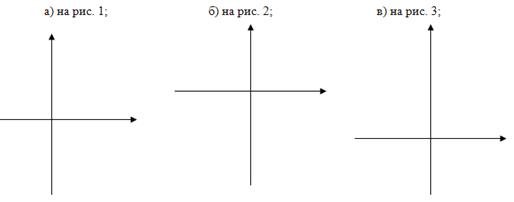
№7. Напишите уравнение функции у= а![]() +m, график которой изображен:
+m, график которой изображен:
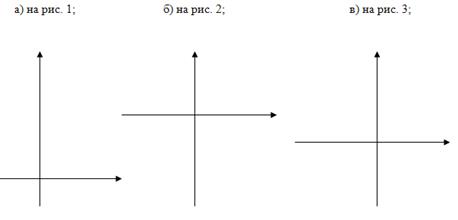
№8. На рисунке построен график функции у= ![]() х². Запишите, как построить, и постройте график функции:
х². Запишите, как построить, и постройте график функции:
1) у= ![]() х²+3; 2) у=
х²+3; 2) у= ![]() х²-5.
х²-5.
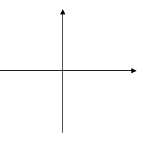
Пример: На рисунке построен график функции у= ![]() х². Запишите, как построить, и постройте график функции у=
х². Запишите, как построить, и постройте график функции у= ![]() х²-7.
х²-7.
Решение. Если функция у= х² при х=m принимает значение f(m)=q, то функция у= ![]() х²-7 принимает при том же х значение на 7 меньше, чем q.
х²-7 принимает при том же х значение на 7 меньше, чем q.
Это значит, что каждая точка графика у= ![]() х² смещается параллельно оси ординат на 7 единиц вниз.
х² смещается параллельно оси ординат на 7 единиц вниз.
Постройте график функции у= ![]() х², сдвигая точки построенного графика у= х².
х², сдвигая точки построенного графика у= х².
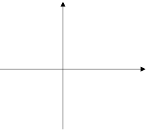
№9. На рисунке построен график функции у= ![]() . Запишите, как построить, и постройте график функции:
. Запишите, как построить, и постройте график функции:
1) у= ![]() +2; 2) у=
+2; 2) у= ![]() -3.
-3.
Пример: На рисунке построен график функции у= ![]() . Запишите, как построить, и постройте график функции у=
. Запишите, как построить, и постройте график функции у= ![]() -1.
-1.
Решение. Если функция у= ![]() при х=m принимает значение f(m)=q, то функция у=
при х=m принимает значение f(m)=q, то функция у= ![]() -1 принимает при том же х=m значение на 1 меньшее, чем q.
-1 принимает при том же х=m значение на 1 меньшее, чем q.
Это значит, что каждая точка графика у= ![]() смещается параллельно оси ординат на 1 единицу вниз.
смещается параллельно оси ординат на 1 единицу вниз.
Постройте график функции у= ![]() , сдвигая точки построенного графика у=
, сдвигая точки построенного графика у= ![]() .
.
№10. На рисунке построен график функции у= 2![]() . Запишите, как построить, и постройте график функции:
. Запишите, как построить, и постройте график функции:
1) у= 2![]() +4; 2) у= 2
+4; 2) у= 2![]() -2.
-2.
Пример: На рисунке построен график функции у= 2![]() . Запишите, как построить, и постройте график функции у= 2
. Запишите, как построить, и постройте график функции у= 2![]() -3.
-3.
Решение. Если функция у= 2![]() при х=m принимает значение f(m)=q, то функция
при х=m принимает значение f(m)=q, то функция
у= 2![]() -3 принимает при том же х= m значение на 3 меньше, чем q.
-3 принимает при том же х= m значение на 3 меньше, чем q.
Это значит, что каждая точка графика у= 2![]() смещается параллельно оси ординат на 3 единицы вниз.
смещается параллельно оси ординат на 3 единицы вниз.
Постройте график функции у= 2![]() -3, сдвигая точки построенного графика у=2
-3, сдвигая точки построенного графика у=2![]() .
.
№11. Решите графически систему уравнений:
а) х²-2у = 0 б) у= 5х²-2 в) у=![]() +2
+2
Новое в образовании:
Особенности формирования пространственных
представлений у детей с задержкой психического развития
Первоначальным источником познания человека является чувственное восприятие, полученное из опыта и наблюдений. В процессе чувственного познания формируются представления, образы предметов, их свойств и отношений. Понимание логических определений, понятий находятся в прямой зависимости от того, как ...
Взаимосвязь общения и идентичности
Общение является важнейшим источником самовосприятия. В свою очередь, некоторые особенности общения могут приводить к содержательным и структурным изменениям идентичности. Например, Р.М. Грановская и Ю.С. Крижанская (1994) считают, что такие особенности педагогического общения, как необходимость оц ...
Современное рабочее место преподавателя на примере кабинета физики
Пример организации рабочего места преподавателя физики в современной школе - полный комплекс ТСО - это качественно новая модель совокупности средств информационных технологий учебного назначения, сочетающих в себе воедино демонстрационные средства, средства индивидуальной работы учащихся и техничес ...
НАВИГАЦИЯ
- Главная
- Работа социального педагога с семьей
- Традиционные основы народной педагогики
- Процесс обучения как целостное явление
- Индивидуальный подход в воспитании детей
- Детские игровые площадки
- Особенности учебного процесса в высшей школе
- Педагогика и воспитание
