Методическая система по формирования математических понятий: множества, величины, числа, алгебраических и геометрических понятий

Таким образом, существует два подхода к понятию натурального числа:

- теоретико-множественный (количественная теория) и аксиоматический (порядковая теория), которые тесно переплетаются в методике преподавания. Поэтому, чтобы избежать ошибок, учитель должен знать, какой из подходов лежит в основе изучения конкретного вопроса.

Теоретико-множественный подход к понятию натурального числа базируется на понятиях конечного множества и взаимно-однозначного соответствия. Приведем схему введения натуральных чисел.

1. Определение. Два конечных множества называются равночисленными, если между ними можно установить взаимно-однозначное соответствие.

2. Отношение "быть равночисленным" разбивает все конечные множества на классы эквивалентности.

3. Каждый класс эквивалентности характеризуется мощностью, поэтому каждому множеству данного класса приписывают как характеристику одно и то же натуральное число.

4. Мощность пустого множества принимается за натуральное число ноль.

Понятие "быть равночисленным" и умение разбивать конечные множества на классы эквивалентности формируется у детей в дочисловой период при изучении темы "Столько, больше, меньше". Покажем, как на основе практической деятельности учащихся можно сформировать понятия о натуральных числах от 0 до 10.

Пример 1. Тема урока "Число и цифра 3".

На одной полке наборного полотна два кружочка, на второй - три, третья полочка пустая (рис. 2.17). Учитель, показывая разные конечные множества, просит разложить их по полкам, т.е. предлагает выполнить классификацию.

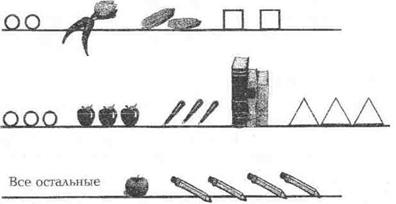
Рис. 2.17

После этого задаются вопросы:

1. Одинаковые ли группы предметов на второй полке? - Нет.

2. Почему же вы их поставили на одну полку? - Количество предметов у них одинаковое.

Учитель делает вывод о том, что это свойство (количество элементов каждого множества данного класса) и есть число 3.

Затем учитель показывает написание цифры 3, т.е. значка, с помощью которого изображается число три.

Следующий этап урока - закрепление. Учитель предлагает найти в классной комнате множество, содержащее по три элемента; выполнить с помощью заданной мерки измерение длины отрезка или площади геометрической фигуры, В этом случае число выступает в новом качестве: оно выражает отношение одной величины к другой. Так, выполняя задание по измерению емкости банки с помощью кружки, ученики получают натуральное число как результат отношения одной емкости к другой. Такой подход приводит к расширению понятия о положительном числе, так как результатом измерения может быть натуральное число, дробное число (положительное рациональное), иррациональное число. Таким образом, рассматривая с первого класса натуральное число как результат измерения величин, ученики постигают причины возникновения любого положительного действительного числа, что очень важно для последующего обучения в школе.

Пример 2. Тема урока "Число нуль".

Учитель задает вопросы типа: "Сколько холодильников в классе?", "Сколько грузовых автомобилей в классе?", Дети отвечают, что этого ничего нет. Тогда учитель говорит, что это соответствует числу нуль и можно записать с помощью цифры 0.

Аксиоматический подход к понятию "натуральное число" базируется на следующих основных (неопределяемых) понятиях: "натуральное число" с выделенным числом "О" (или "I") и "непосредственно следовать за ,".

В целом ряде книг за выделенное число принимается число 1. На наш взгляд целесообразнее выделять число 0, так как методика его введения аналогична методике выделения любого однозначного натурального числа (см. примеры 1 и 2). Кроме того, легче вводить тогда использование линейки.

Новое в образовании:

Развитие логической мышления при изучения раздела «Основы алгоритмизации»
В основе системы знаний учащихся лежит сформированность системы понятий изучаемой предметной области. Владение понятийным аппаратом в большей степени определяет понимание учебного материала, его использование для решения прикладных задач. Каждое новое вводимое понятие должно быть четко определено, ...

Психолого-педагогические основы воспитания нравственных ценностей у старшеклассников
Практика воспитания личности своими корнями уходит в глубинные пласты человеческой цивилизации. В воспитании и развитии личности особое место занимают внутренние духовно-нравственные ценности. Ценности и идеалы тесно связаны с историческими факторами. В связи со сменой классов менялись представлени ...

Средства мультимедиа в образовательном процессе
Многие преподаватели впервые сталкиваются с понятием мультимедиа, когда в их распоряжении оказывается компьютер, оснащенный специальным оборудованием, позволяющий работать с самой разнообразной информацией, такой как текст, звук, неподвижные и движущиеся изображения. Для большинства людей, имеющих ...