Методическая система по формирования математических понятий: множества, величины, числа, алгебраических и геометрических понятий

Дети убеждаются, что отрезок CD не помещается в AB целое число раз. Тогда им предлагается в качестве мерки отрезок МК, с помощью которого они измеряют отрезки AB и CD. Пусть в отрезке AB отрезок МК помещается 4 раза, а в отрезке CD – 3 раза. Значит, отрезок МК является 1/3 частью отрезка CD и поэтому в отрезке AB отрезок CD помещается 5/3 раза. Таким образом, в результате измерения отрезка AB отрезком CD получилась дробь 5/3.

Примечание. Еще в глубокой древности ученые пришли к выводу, что существуют и величины, которые не имеют общей мерки. Таким образом, в результате измерения могут получиться натуральные числа, дробные числа (положительные рациональные числа) и иррациональные числа, то есть любое положительное действительное число есть результат измерения величин. Поэтому измерению различных величин в начальных классах должно быть уделено серьезное внимание.

Требования к измерению величин.

1. Равным однородным величинам должно быть поставлено в соответствие единственное число.

Формирование в начальных классах этого требования к измерению величин осуществляется в следующей последовательности:

а) визуальное сравнение;

б) опосредованное сравнение;

в) создание проблемной ситуации: как быть, если ни визуально, ни опосредованно сравнить нельзя. Ученики подводится к выводу, что нужно сравнить числа, которые получаются в результате измерения.

Примеры практических работ на визуальное сравнение, опосредованное сравнение, необходимость измерения величин были приведены выше.

Из множества однородных величин выбирается одна, которой ставится в соответствие число один.

Здесь важно показать, что за единицу измерения может быть взят любой элемент. Однако, если одинаковые по величине элементы будут измеряться разными единицами измерения, то полученные числа не помогут сделать верный вывод по сравнению этих элементов. Этот момент можно сформировать у учащихся с помощью следующей практической работы.

Пример 1. Учитель показывает три одинаковые полоски красного, белого и черного цветов и просит, не накладывая их назвать, какая из них короче, а какая – длиннее. Дети называют черную полоску самой короткой, а белой – самой длинной. Тогда, раздав одному ряду красные полоски, другому – белые, третьему черные, учитель просит измерить их мерками (полосками), которые заранее розданы на парты. В результате измерения красных полосок дети получают число 3, черных – 4, белых – 2. После этого учитель наложением полосок убеждает детей, что они одинаковой длины, и задает вопрос: «Почему в результате измерения получились разные числа?» Учащиеся приходят к выводу, что нужно договориться и измерять одинаковыми мерками (единицами измерения). После этого можно провести беседу о разных единицах измерения длин.

Пример 2. Аналогичную работу можно провести по измерению площадей, взяв одинаковые листы бумаги белого, черного и красного цветов, а за единицу измерения белого листа бумаги взять 1/2 листа, красного листа бумаги –1/4 листа, черного листа бумаги – 1/8.

Если величина «а» есть сумма величин «b» и «c», то ее мера равна сумме их мер.

Сформировать это требование можно при помощи следующих практических работ.

Пример 1. Надо перевязать пакет с помощью нескольких коротких веревочек. Ученики связывают нужное количество обрывков и перевязывают пакет. Дается задание: какой длины веревку нужно взять оператору почты, чтобы перевязать пакет такого же размера, если веревку связали из трех кусков длиной 10 см, 15 см и 30 см. Дети находят: 10см +25см +30 см =55 см.

Пример 2. Нужно сравнить две геометрических фигуры разной формы (рис. 2.12). В ходе измерения дети приходят к выводу, что фигуры равновелики, так как они равносоставлены.

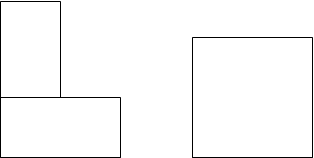Новое в образовании:

Методы диагностики нарушений звукопроизношения при дизартрии
Особенностью дизартрии у детей является чаще всего ее смешанный характер (сочетание различных клинических синдромов). Наряду с нарушением звукопроизношения проявляются другие речевые расстройства (задержка речевого развития, общее недоразвитие речи, моторная алалия, заикание). Кроме того, страдает ...

Становление мировоззрения личности подростка
Интенсивное формирование личности в подростковом возрасте делает этот процесс достаточно благоприятным для овладения диалектико-материалистической концепцией мира. Изучая систематические курсы основ наук, подростки совершают более глубокий анализ предметов и явлений реальной действительности, наход ...

Учет индивидуальных особенностей детей в воспитании
Проблеме индивидуального подхода в воспитании детей уделяли внимание многие представители прогрессивной педагогики, как русской, так и зарубежной. Уже в педагогической системе Я.А.Коменского – великого чешского педагога – четко обозначены положения о том, что весь процесс обучения и воспитания дете ...