Методическая система по формирования математических понятий: множества, величины, числа, алгебраических и геометрических понятий

Свойства этих основных понятий, соотношение между ними раскрываются в аксиомах Пеано (итальянский математик). Приведем некоторые из них.

Аксиома 1. Нуль непосредственно не следует ни за каким натуральным числом.

Эта аксиома формируется у учащихся при пользовании линейкой для измерения длины отрезка: учитель подчеркивает, что линейку надо прикладывать так, чтобы начало отрезка совпадало с делением 0.

Аксиома 2. Для любого натурального числа существует только одно натуральное число, которое непосредственно следует за ним.

Эта аксиома формируется у учащихся с помощью вопросов: "Какое число идет за числом V ? "Может ли за числом 2 идти число 5 ?"

Аксиома 3. Любое натуральное число непосредственно следует не более чем за одним натуральным числом.

Эта аксиома формируется у детей с помощью вопросов: "За каким числом идет число 5 ?", "Может ли число 5 идти за числом 3 ?", "За каким числом идет число О?"

Таким образом, аксиоматический подход к понятию натурального числа позволяет охарактеризовать следующие свойства натурального ряда чисел (порядковую структуру множества натуральных чисел).

1. Множество натуральных чисел бесконечно, с начальным элементом О и без конечного элемента.

2. Множество натуральных чисел упорядочено (любые два натуральных числа можно сравнить). "

3. Множество натуральных чисел дискретно (между двумя любыми натуральными числами можно поместить конечное множество натуральных чисел).

V. Операции над натуральными числами

Ранее уже неоднократно подчеркивалось, что в методике обучения операциям над натуральными числами следует отличать саму операцию от результата операции.

Смысл операций над натуральными числами и их законы формируются на теоретико-множественной основе. Нахождение результата операций раскрывается в аксиоматической теории. Так, операции сложения и умножения натуральных чисел базируется на следующих аксиомах

Операция сложения Операция умножения.

1. а + 0 = а; 3. а • 0 = 0;

2. а + b' я (а + b)' 4. а • b' = а ' b + а . Следствие: а + 1 = а' . Следствие: а • 1 =5 а .

Аксиомы 1 и 3 и следствия из этих аксиом ученики должны твердо знать Нахождение результата сложения (до таблиц сложения) определяется путем присчитывания по одному (т.е. используется первое следствие).

Нахождение результата умножения в начальных классах нельзя рассматривать с позиции аксиом 3 и 4. Поэтому в традиционной методике умножение рассматривается как частный случай сложения, что позволяет умножать натуральные числа только начиная с двух. Естественно, такой подход к операции умножения нельзя считать удачным, так как не позволяет найти результат умножения в таких случаях, как а • 1; а - 0;

(а/b) • (с/а).

В разделах I и III достаточно подробно рассмотрена операция умножения как мощность декартова произведения и как сумма одинаковых величин. Существует и другой подход к операции умножения, с позиции которого можно обосновать не только умножение натуральных чисел, начиная с двух, но и умножение на 1 и на 0, умножение обыкновенных дробей. Этот подход заключается в том, что умножение рассматривается как переход от одной единицы измерения к другой Сформировать у учащихся смысл операции умножения с этой позиции можно на таких практических работах.

Пример 1. Нужно измерить емкость банки сначала кружками, а потом стаканами (рис. 2.18). В ходе измерения получили 5 кружек или 15 стаканов. Учитель обращает внимание на то, что стаканами измерять долго, и задает

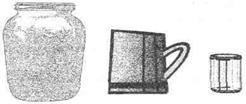
Рис. 2.18

вопрос: "Нельзя ли узнать, не измеряя, сколько стаканов в банке?" Дети предлагают для этого измерять стаканами кружку. Так как в банке 5 кружек (старая мерка) и в одной кружке 3 стакана (новая мерка), то в банке 5 • 3 = 15 (стаканов).

Новое в образовании:

Эффективность коррекционной программы по развитию коммуникативной компетентности у подростков, имеющих нарушения интеллекта
Процесс развития коммуникативной компетентности у подростков происходит в активной деятельности с другими детьми, здесь он приобретает свой эмоциональный и социальный опыт общения, он чувствует расположение к себе, любовь или равнодушие, теплоту или холодность, сердечность или отстраненность. Таког ...

Урок – основная форма организации обучения в современной школе
Более или менее законченный отрезок педагогического процесса в классно-урочной системе обучения — это урок. По образному выражению Н.М.Верзилина, «урок — это солнце, вокруг которого, как планеты, вращаются все другие формы учебных занятий». Что такое урок? Ответ на этот вопрос весьма затруднителен ...

Определение функции
Начиная с XVII в. одним из важнейших понятий является понятие функции. Оно сыграло и поныне играет большую роль в познании реального мира. Идея функциональной зависимости восходит к древности, она содержится уже в первых математически выраженных соотношениях между величинами, в первых правилах дейс ...