Методические основы обучения координатному методу

Этапы решения задач методом координат

Чтобы решать задачи как алгебраические, так и геометрические методом координат необходимо выполнение 3 этапов:

1) перевод задачи на координатный (аналитический) язык;

2)преобразование аналитического выражения; Самая подробная информация санкт-петербург красносельский район у нас на сайте.

3)обратный перевод, т. е. перевод с координатного языка на язык, в терминах которого сформулирована задача.

Для примера рассмотрим алгебраическую и геометрическую задачи и проиллюстрируем выполнение данных 3 этапов при их решении координатным методом.

№1. Сколько решений имеет система уравнений.

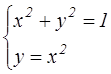
Решение:

1 этап: на геометрическом языке в данной задаче требуется найти, сколько точек пересечения имеют фигуры, заданные данными уравнениями. Первое из них является уравнением окружности с центром в начале координат и радиусом, равным 1, а второе — уравнением параболы.

2 этап: построение окружности и параболы; нахождение точек их пересечения.

3 этап: количество точек пересечения окружности и параболы является ответом на поставленный вопрос.

№2. Найдите множество точек, для каждой из которых расстояния от двух данных точек равны.

Решение:

Обозначим данные точки через А и В. Выберем систему координат так, чтобы ось Ох совпадала с прямой АВ, а началом координат служила точка А Предположим далее, что АВ=а, тогда в выбранной системе координат А(0,0) и В(а,0). Точка М(х,у) принадлежит искомому множеству тогда и только тогда, когда АМ=МВ, или, что то же самое, АМ2=МВ2. Используя формулу расстояния от одной точки координатной плоскости до другой, получаем АМ2=x2+y2, MB2=(x-a)2+y2. Тогда х2+у2=(х-а)2 + у2

Равенство х2+у2=(х-а)2+у2 и является алгебраической моделью ситуации, данной в задаче. На этом заканчивается первый этап ее решения (перевод задачи на координатный язык).

На втором этапе осуществляется преобразование полученного выражения, в результате которого получаем соотношение .

На третьем этапе осуществляется перевод языка уравнения на геометрический язык. Полученное уравнение является уравнением прямой, параллельной оси Оу и отстоящей от точки А на расстояние , т.е. серединного перпендикуляра к отрезку АВ.

Задачи, обучающие координатному методу

Для разработки методики формирования умения применять координатный метод важно выявить требования, которые предъявляет логическая структура решения задач мышлению решающего. Координатный метод предусматривает наличие у обучающихся умений и навыков, способствующих применению данного метода на практике. Проанализируем решение нескольких задач. В процессе этого анализа выделим умения, являющиеся компонентами умения использовать координатный метод при решении задач. Знание компонентов этого умения позволит осуществить его поэлементное формирование.

Задача №1 . В треугольнике ABC: AC=b, AB=c, ВС=а, BD - медиана. Докажите, что .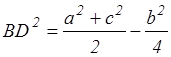

Выберем систему координат так, чтобы точка А служила началом координат, а осью Ох - прямая АС (рис. 2).

(умение оптимально выбирать систему координат, т. е. так, чтобы наиболее просто находить координаты данных точек).

В выбранной системе координат точки А, С и D имеют следующие координаты: А(0,0), D(,0) и С(b,0)

(умение вычислять координаты заданных точек). Обозначим координаты точки В через х и у. Тогда используя формулу для нахождения расстояний между двумя точками, заданными своими координатами, получаем:

х2+у2=с2 , (x-b)2+y2=a2 (1)

(умение находить расстояние между двумя точками, заданными координатами)

По той же формуле . (2)

Используя формулы (1) находим х и у.

Они равны:

; .

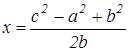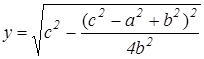Далее, подставляя х и у в формулу (2), находим .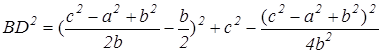

.

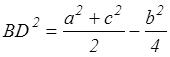(умение выполнять преобразования алгебраических выражений)

Задача №2. Найти множество точек, для каждой из которых разность квадратов расстояний от двух данных точек есть величина постоянная.

Новое в образовании:

История и разновидности декупажа
Декупаж (Decoupage или découpage) – это искусство украшения предметов путем наклеивания элементов из цветной бумаги. Они сочетаются со специальными эффектами, такими как раскрашивание, вырезание, покрытие сусальным золотом и прочее. Обычно какой-либо предмет, например, небольшие коробки или ...

Общеметодический подход к формированию математических понятий в школьной практике
В школьной практике многие учителя добиваются от учеников заучивания определений понятий и требуют знания их основных доказываемых свойств. Однако результаты такого обучения обычно незначительны. Это происходит потому, что большинство учащихся, применяя понятия, усвоенные в школе, опираются на мало ...

Анализ работы по развитию творческого воображения в изобразительной деятельности у детей с задержкой психического развития
Таблица 9. Анализ полученных результатов учащихся 2б класса по методике «Несуществующее животное» № п/п Имя учащегося Уровень творческого воображения 1 2 3 1. Тима М. 1 2. Игорь П. 1 3. Даяна Б. 2 4. Виталик С. 1 5. Дима Я. 1 6. Артем К. 1 Анализ результатов: 83,3% учащихся имеют I уровень; 16,6% у ...