Методические основы обучения координатному методу

Решения этих задач были разобраны выше.

Несмотря на недостатки метода координат такие как наличие большого количества дополнительных формул, требующих запоминания, и отсутствие предпосылок развития творческих способностей учащихся, некоторые виды задач трудно решить без применения данного метода. Поэтому изучение метода координат необходимо, однако более детальное знакомство с этим методом целесообразно проводить на факультативных занятиях. Далее приведем ряд задач для факультативов.

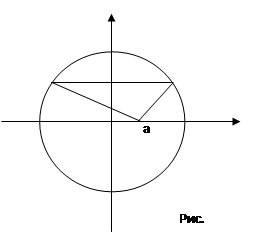Пример 1. Докажите, что сумма квадратов расстояний от точки, взятой на диаметре окружности, до концов любой из параллельных ему хорд постоянна.

Решение:

Введем прямоугольную систему координат с началом в центре окружности. Пусть хорда МР параллельна оси Ох, а точка А принадлежит диаметру (рис. 11). Обозначим расстояние ОА через а, а расстояние от точки Р до оси Ох через b. Тогда точка А имеет координаты (а, 0). Точки Р и М принадлежат окружности с центром в начале координат и радиусом равным 1, следовательно их координаты удовлетворяют уравнению данной окружности . Используя это уравнение находим координаты точек Р() и М(). Необходимо доказать, что АМ2+АР2 не зависит от переменной b. Найдем АМ2 и АР2 используя формулу нахождения расстояния между двумя точками по их координатам: . Они соответственно равны и , а их сумма после приведения подобных равна 2а2+2. Это число не зависит от переменной b, что и требовалось доказать.

Пример 2. Доказать, что сумма квадратов длин сторон четырехугольника равна сумме квадратов длин его диагоналей, сложенной с учетверенным квадратом расстояния между серединами диагоналей. (Теорема Эйлера)

Решение: Введем прямоугольную систему координат как показано на рисунке 12.

Пусть точки А, В, С и D имеют координаты (0,0), (d,0), (c,d) и (0,d) соответственно. Следовательно, координаты точек L и P есть () и (). Найдем квадраты длин отрезков, с помощью формулы нахождения расстояния между точками по их координатам.

AD2=; BC2=; DC2=; AB2=;

AC2=; BD2=; LP2=.

Запишем выражение, которое необходимо доказать, используя найденные нами значения.

AD2+BC2+DC2+AB2=AC2+BD2+4LP2

+++=++4

Раскроем скобки, приведем подобные и получим верное равенство 0=0. Значит, сумма квадратов длин сторон четырехугольника равна сумме квадратов длин его диагоналей, сложенной с учетверенным квадратом расстояния между серединами диагоналей.

Пример 3. Диаметры AB и CD окружности перпендикулярны. Хорда ЕА пересекает диаметр СD в точке К, хорда ЕС пересекает диаметр АВ в точке L. Докажите, что если СК:KD так же как 2:1, то AL:LB так же как 3:1.

Решение: Введем прямоугольную систему координат, направив оси по данным диаметрам AB и CD (рис. 13).

Радиус окружности будем считать равным 1. Тогда точки А, В, С, D будут иметь координаты (-1,0), (1,0), (0,-1), (0,1) соответственно. Так как СК:KD=2:1, то точка К имеет координаты (0,). Найдем координаты точки Е как точки пересечения прямой АК, имеющей уравнение и окружности, заданной уравнением . Получаем, что точка Е имеет координаты (). Точка L – это точка пересечения прямых СЕ и оси абсцисс, значит ординаты точки L равна 0.

Новое в образовании:

Процесс и основные результаты опытно-экспериментальной работы по воспитанию классным руководителем нравственных ценностей у старшеклассников
Опытно-экспериментальную работу мы рассматриваем как целостный процесс, включающий комплекс методов исследования, который обеспечивает научную, объективную и доказательную проверку правильности обоснованной в начале исследования гипотезы. Задачами опытно-экспериментальной работы явилось: изучить со ...

Режим дня ребёнка
После года у ребенка возрастает потребность в более продолжительном бодрствовании, но какое-то время ему подходит режим 9-12 месячного ребенка. Ночью он спит 10-11 часов, днем 2 раза по 1,5-2 часа, ест 4-5 раз через 3,5-4 часа, в основном после сна. С возрастом ребенку уже не хочется есть сразу пос ...

Значение подвижных игр для развития личности ребенка
Игра является основным видом деятельности дошкольника. Она выступает и как форма организации жизни детей в дошкольном учреждении, и как средство их разностороннего развития, и как метод обучения. Игре придается большое значение в социальном становлении личности ребенка, а игровые навыки рассматрива ...