Методические основы обучения координатному методу

Обозначим данные точки через А и В. Выберем систему координат так, чтобы ось Ох совпадала с прямой АВ, а началом координат служила точка А.

(умение оптимально выбирать систему координат).

Предположим АВ=а, тогда в выбранной системе координат А(0,0), В(а,0).

(умение находить координаты заданных точек)

Точка М(х,у) принадлежит искомому множеству тогда только тогда, когда AM2-MB2=b2 где b - постоянная величина

(умение переводить геометрический язык на аналитический, составлять уравнения фигур).

Используя формулу расстояний между двумя точками, получаем:

, ,

(умение вычислять расстояние между точками, заданными координатами), или 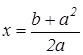. Данное уравнение является уравнением прямой, параллельной оси Оу и отстоящей от точки А на расстояние .

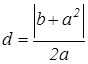(умение видеть за уравнением конкретный геометрический образ)

Нетрудно видеть, что и для решения этой задачи необходимо овладение перечисленными выше умениями. Кроме того, для решения приведенной задачи, а также и других задач важно умение «видеть за уравнением» конкретный геометрический образ, которое является обратным к умению составлять уравнения конкретных фигур.

Выделенные умения являются основой при решении и более сложных задач.

Задача №3. В трапеции меньшая диагональ перпендикулярна основаниям. Найти большую диагональ, если сумма противоположных углов равна , а основания равны а и b.

Направим оси координат по меньшей диагонали и одному из оснований (рис. 3).

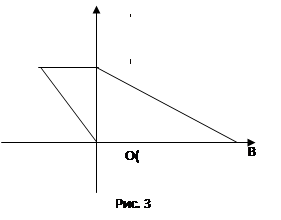(умение оптимально выбирать систему координат).

Тогда точка А имеет координаты (0,0), точка В - (а,0), точка С - (0,c), точка D - (b,c).

(умение находить координаты заданных точек)

Пусть и острые углы в трапеции АВСD, тогда их сумма равна . Для вычисления длины большей диагонали BD надо найти значение с. Его можно вычислить 2 способами. Первый - из прямоугольного треугольника АВС по формуле находим . Второй способ из прямоугольного треугольника ACD: . Отсюда получили, что

(1)

Из равенства (1) находим отношение : оно равно -, так как . Выразим . Он равен , исходя из этого, пользуясь зависимостью (1), получаем .

(умение выразить недостающие координаты через уже известные величины)

Далее воспользовавшись координатной формулой расстояния между двумя точками, найдем длину BD.

(умение вычислять расстояние между точками, заданными координатами)

Она равна .

Итак, компонентами умения применять координатный метод в конкретных ситуациях являются следующие умения:

переводить геометрический язык на аналитический для одного типа задач и с аналитического на геометрический для другого;

стоить точку по заданным координатам;

находить координаты заданных точек;

вычислять расстояние между точками, заданными координатами;

оптимально выбирать систему координат;

составлять уравнения заданных фигур;

видеть за уравнением конкретный геометрический образ;

выполнять преобразование алгебраических соотношений.

Данные умения можно отработать на примере следующих задач, формирующих координатный метод:

задачи на построение точки по ее координатам;

задачи на нахождение координат заданных точек;

задачи на вычисление расстояния между точками, заданными координатами;

Новое в образовании:

Эволюция исследований в области развития речи детей дошкольного возраста
Научные исследования ряда психологов и педагогов показали, что именно дошкольное детство является особенно сензитивным к усвоению речи. Следовательно, лингвистическое воспитание ребенка должно начинаться рано и в первые годы жизни совершаться исключительно на родном языке. Важнейшим условием полноц ...

Сравнительный анализ констатирующего и контрольного экспериментов в контрольной и экспериментальной группах
При анализе результатов констатирующего и контрольного экспериментов, выявилось, что при производственной деятельности (тест «Рукавички») коммуникативные навыки проявляются гораздо выше, чем в ситуациях непосредственного общения («Незавершенная сказка»). Предполагаем, что это связано с тем, что пер ...

Условия эффективного управления дошкольным учреждением, закономерности и принципы педагогического руководства дошкольным учреждением
Управленческая деятельность руководителя дошкольного образовательного учреждения многогранна, пронизывает все происходящие в дошкольном учреждении процессы и отличается большой сложностью и динамизмом. Управление предполагает умелое использование существующих закономерностей, создание хорошо продум ...