Методические основы обучения координатному методу

Длина отрезка АВ равна 5см. а)Выберите систему координат, в которой можно было бы наиболее просто определить координаты концов отрезка. б)Выберите систему координат так, чтобы координаты концов отрезка были бы: А (-2.5,0), В(2.5,0).

Постройте квадрат ABCD со стороной 2 см; отметьте точку М- центр квадрата. Поместите начало координат последовательно в точки A, B, C, D и выберите направление осей координат так, чтобы точка М в каждой системе координат имела координаты (1;1). За единичный примите отрезок длиной 1 см.

Треугольник ABC равносторонний (длина стороны равна 6 см.). Выберите систему координат так, чтобы можно проще было бы определить координаты его вершин.

III. Расстояние между точками

Точка М(а,с) находится от начала координат и точки А(4,0) соответственно на расстояниях 3 и 4 см. Определите координаты точки М.

Дан прямоугольник ABCD (АВ=2 см., ВС=4 см.). Как выбрать систему координат, чтобы его вершины имели координаты А(-1,-2), В(-1,2), С(1,2), D(l,-2)?

Длины сторон треугольника ABC равны 3, 4 и 5 см. Выберете систему координат и определите в ней координаты вершин треугольника ABC.

Вершины четырехугольника ABCD имеют следующие координаты: А(-3,1), В(3,6), С(2,2) и D(-4,3). Установите вид четырехугольника.

IV. Составление уравнения фигур

Это умение является одним из основных умений, которые необходимы при применении метода координат к решению задач.

Изобразите систему координат. Отметьте на оси Ох точки А и В. Запишите соотношения, которым удовлетворяют координаты точек, принадлежащих: а)отрезку АВ; б)лучу АВ; в)лучу ВА;

Запишите уравнение прямой, содержащей начало координат и точку А(2,5).

Запишите уравнение прямой, содержащей точки А(2,7)и В(1,3).

Изобразите на координатной плоскости произвольную прямую и найдите ее уравнение.

Запишите соотношения, которым удовлетворяю координаты точек прямоугольника с вершинами А(2,3), В(2,5), С(4,5), D(4,3).

Что представляют собой множества точек плоскости, координаты которых удовлетворяют неравенствам: а)х≤3; b)-5≤х≤0; c)x>1; d)x<-2; e)≥2; f)≥0?

Какую фигуру образует множество точек, координаты которых удовлетворяют системе неравенств 2≤x≤5 и 1≤y≤3?

Постройте точки, симметричные точкам А(2,-3) , В(5,0), С (0,7) относительно: а) оси Ох; б) оси Оу; в)биссектрисы I и III координатных углов. Запишите эти координаты.

Установите, относительно какой из координатных осей симметричны точки А(1,2), В (-7,2).

Точки А(5,…), В(…,2) симметричны относительно оси Ох. Запишите пропущенные координаты.

Постройте образы точек А(1,5), В(-2,3), С(3,0) при параллельном переносе а)О(0,0)→К(3,0); 6)0(0,0)→М(2,3). Запишите их координаты.

С помощью какого параллельного переноса можно отобразить точку М(-3,4) в точку M1(2,4)?

Найдите на прямых у=-Зх+1 и у=2х+3 точки, симметричные относительно оси Ох.

Запишите уравнение прямой, на которую отображается прямая у=4х-3 вектором с координатами (3,4).

На прямых у=Зх+2 и у=-5х+5 найдите такие точки, которые находятся одна от другой на расстоянии 5 см, и принадлежат прямой, параллельной оси Ох.

Виды задач, решаемых методом координат

Применяя метод координат, можно решать задачи двух видов.

Пользуясь координатами можно истолковать уравнения и неравенства геометрически и таким образом применять геометрию к алгебре и анализу. Графическое изображение функции первый пример такого применения метода координат.

Задавая фигуры уравнениями и выражая в координатах геометрические соотношения, мы применяем алгебру к геометрии. Например, можно выразить через координаты основную геометрическую величину - расстояние между точками.

В связи с усилением роли координатного метода в изучении геометрии особенно актуальной становиться проблема его формирования. Наиболее распространенными среди планиметрических задач, решаемых координатным методом, являются задачи следующих 2 видов: 1) на обоснование зависимостей между элементами фигур, особенно между длинами этих элементов; 2) на нахождение множества точек, удовлетворяющих определенным свойствам.

Примером задач первого вида может служить следующая:

«В треугольнике ABC, AB=c, AC=b, BC=a, BD - медиана.

Доказать, что »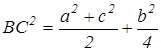

Задача: «Найти множество точек, для каждой из которых разность квадратов расстояний от двух данных точек есть величина постоянная» - является примером задач второго вида.

Новое в образовании:

Процесс и основные результаты опытно-экспериментальной работы по воспитанию классным руководителем нравственных ценностей у старшеклассников
Опытно-экспериментальную работу мы рассматриваем как целостный процесс, включающий комплекс методов исследования, который обеспечивает научную, объективную и доказательную проверку правильности обоснованной в начале исследования гипотезы. Задачами опытно-экспериментальной работы явилось: изучить со ...

Анализ работы по развитию творческого воображения в изобразительной деятельности у детей с задержкой психического развития
Таблица 9. Анализ полученных результатов учащихся 2б класса по методике «Несуществующее животное» № п/п Имя учащегося Уровень творческого воображения 1 2 3 1. Тима М. 1 2. Игорь П. 1 3. Даяна Б. 2 4. Виталик С. 1 5. Дима Я. 1 6. Артем К. 1 Анализ результатов: 83,3% учащихся имеют I уровень; 16,6% у ...

Понятие о ДЦП. Виды и формы ДЦП. Прогноз
Детский церебральный паралич (ДЦП) - тяжёлое мультифакториальное заболевание нервной системы, обусловленное вредоносными воздействиями на мозг в различные периоды внутриутробного развития ребёнка, во время родов и в первые недели жизни. Время воздействия вредоносных факторов определяет картину боле ...