Методические основы обучения координатному методу

Найдем абсциссу точки L. Прямая СЕ задана уравнением . Она пересекает ось Ох в точке (,0). Отсюда координаты точки L(,0). Найдем отношение AL:LB. Оно равно трем, что и требовалось доказать.

Задачи

Доказать, что если в треугольнике две медианы конгруэнтны, то треугольник равнобедренный.

Найти множество таких точек Р, что отношение расстояний от каждой из них до двух данных точек равно а.

Докажите, что уравнение окружности с центром в точке С (а,с) и радиусом r имеет вид: (х-а)2+(у-с)2=r2

Найти угол между прямыми Зх-4у+6=0 и 12х+5у+8=0

Определите расстояние от точки А(-3,4) до прямой у=х+2.

Вычислите площадь треугольника, вершины которого имеют следующие координаты: А (0,-2), В(6,2) и С(2,4) .

На прямой с даны три точки А, В, С так, что точка В лежит между точками А и С. В одной полуплоскости с границей а построены равносторонние треугольники АМВ и ВРС. Доказать, что середина отрезка РА, середина отрезка МС и точка В являются вершинами равностороннего треугольника.

Доказать, что для любой точки Р лежащей между вершинами В и треугольника ABC, справедливо равенство :

АВ2*РС+АС*ВР-АР2*ВС=ВС*ВР*РС.

Дан прямоугольник. Докажите, что сумма квадратов расстояний от произвольной точки, принадлежащей плоскости этого прямоугольника до его вершин, в два раза больше суммы квадратов расстояний от этой точки до сторон прямоугольника.

Доказать, что если через некоторую точку М провести прямую, пересекающую окружность в точках А и В, то произведение МА*МВ постоянно и не зависит от положения прямой.

Дан прямоугольник ABCD. Найти множество точек М, для которых MA2+MC2=MB2+MD2. (ответ: множество точек М есть плоскость)

Дан прямоугольник ABCD. Найти множество точек М, для которых MA+MC=MB+MD. (Ответ: пара прямых)

Дан прямоугольный треугольник ABC (ÐC=90°) . Найти множество точек Р, для которых 2РС2=РА2+РВ2. (ответ: множество точек Р есть прямая, содержащая середину М гипотенузы АВ и перпендикулярная к медиане СМ).

Опытное преподавание проводилось в 9 классе средней общеобразовательной школы №51. Перед его проведением была изучена математическая и методическая литература и разработана методика проведения факультатива. Было проведено 2 занятия. В данном классе изучение геометрии ведется по учебнику [2], поэтому в качестве основного теоретического и практического источника я выбрала данный методический комплект.

I. Занятия проводились по теме «Простейшие задачи в координатах», до ознакомления с которыми учащиеся изучали тему «Векторы», познакомились с понятием «координаты вектора», а также узнали формулу середины отрезка.

1 занятие: «Простейшие задачи в координатах»

Образовательная цель урока – рассмотреть задачи о вычислении длины вектора по его координатам и по координатам его начала и конца; показать, как они используются при решении других задач.

Содержание урока:

Вначале урока был проведен устный счет для проверки усвоения материала, разобранного на прошлом уроке, а также для проведения пропедевтической работы по повторению тех понятий и фактов, которые будут использованы при объяснении нового материала.

Устный счет:

Координаты точек А(-2, 3) и В(2, -4). Найдите координаты векторов и .

Координаты точек М(5,-8) и Р(-3, 4). Найдите координаты точки О (О – середина отрезка МР).

СР – диагональ окружности; С(-2, -1), Р(5, 7). Найдите координаты центра окружности – точки Е.

ABCD – прямоугольник, АD=7, АВ=5. Найдите АС.

Новый материал:

Вычисление длины вектора по его координатам.

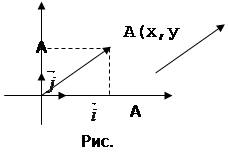
Вывод формулы опирается на теорему Пифагора и на то, что расстояние между двумя точками оси координат находится по формулам (для точек ; оси х) и (для точек ; оси у). Покажем, что длина вектора равна . Данная формула доказывается только для случая, когда х≠0 и у≠0, в достоверности других случаев учащимся предоставляется убедиться самостоятельно. Для доказательства задаем координатную плоскость и рассматриваем вектор с началом в начале координат (по теореме: от любой точки можно отложить вектор, равный данному и притом единственный). Используя формулу для нахождения координат вектора по координатам его начала и конца, можем найти координаты точки А. Далее с помощью теоремы Пифагора находим длину отрезка ОА=. следовательно, их длины раны, т.о. .

Новое в образовании:

Влияние дидактической игры на познавательную деятельность детей старшего дошкольного
«Концепция дошкольного воспитания» (авторы В.В. Давыдов, В.А. Петровский и др.) – ориентируют педагогов на гуманизацию воспитательно-образовательного процесса детского сада через «…реализацию специфических возрастных возможностей психического развития дошкольников … в соответствующих возрасту видах ...

Виды мышления
Система приемов и способов умственной деятельности помогает учащимся обнаружить, выделить, объединить существенные признаки изучаемых предметов и явлений. В психологии рассматривают следующие виды мышления (табл.1). Таблица 1 Организация мыслительной деятельности Виды мышления По форме наглядно-обр ...

Особенности декоративно – прикладного искусства в работе с детьми старшего дошкольного возраста
К наиболее ярким особенностям народного прикладного искусства следует отнести необыкновенно меткие, продуманные и правдивые характеристики конкретного образа, переданного в большой выразительности, прием форма, в которую вкладывает народный мастер свой замысел, всегда предельно лаконична. Все второ ...