Методические основы обучения координатному методу

задачи на оптимальный выбор системы координат;

задачи на составление уравнения фигуры по ее характеристическому свойству;

задачи на определение фигуры по ее уравнению;

задачи на преобразование алгебраических равенств;

Приведем примеры таких задач. BBUS. Выгодная аренда микроавтобуса с водителем на любой срок.

I. Построение точек на плоскости.

С координатной прямой, а затем и с координатной плоскостью учащиеся знакомятся в 5-6 классах при изучении математического материала. При этом удобно использовать мультимедийные презентации, которые позволяют в динамике излагать необходимый материал, использовать всевозможные иллюстрации и звуковые эффекты, тем самым, заинтересовывая учащихся и являясь хорошим наглядным средством. Одним из примеров является презентация «Метод координат», опирающаяся на учебник. Приведем несколько примеров задач, которые можно использовать при изучении координатной плоскости. Эти задачи могут быть использованы:

для оттачивания навыков построения точек по их координатам со всем классом;

для дополнительных заданий отстающим ученикам;

для развития интереса к изучаемой теме.

На координатной плоскости постройте точки А(7,2), B(-2,1), C(0,2).

Отметьте на плоскости несколько точек. Начертите произвольную систему координат и найдите в ней координаты заданных точек.

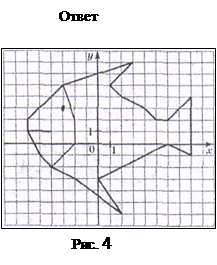Постройте фигуры по координатам их узловых точек. Указание: узловыми будем называть точки, служащие концами отрезков, образующих фигуры. Точки, координаты которых записаны подряд через запятую, соединяйте последовательно друг с другом. Если же координаты разделяются знаком «;», то соответствующие точки не следует соединять. Они нужны для изображения вспомогательных элементов.

А) Камбала (Рис. 4)

(3,7), (1,5), (2,4), (4,3),

(5,2), (6,2), (8,4), (8,-1),

(6,0), (0,-3),(2,-6),(-2,-3),

(-4,-2),(-5,-1),(-6,1),(-4,1);

(-6,1), (-6,2), (-3,5), (3,7);

(-4,-2),(-2,0),(-2,2),(-3,5);(-3,3).

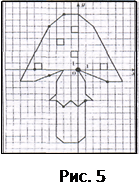
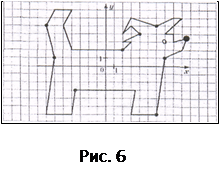
Б)Найдите координаты выделенных на рисунке точек, двигаясь по часовой стрелке от самой жирной точки. (Рис. 5 и 6)

II.Задачи на выбор системы координат

Выбор системы координат имеет очень важное значение при применении метода координат.

Для примера возьмем задачу, которая рассмотрена в учебнике «Середина гипотенузы прямоугольного треугольника равноудалена от его вершин».

Первым шагом при применении метода координат является такой выбор осей и системы координат, при котором алгебраические выкладки становятся более простыми. Для данной задачи удачный выбор системы координат показан на рисунке 7. Таким образом, начало координат помещаем в точку А, а оси проводим через точки В и С так, чтобы эти точки лежали на положительных лучах осей. Следовательно, В(а,0) и С(0,b). Поэтому по формуле середины отрезка D(). Теперь , .

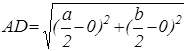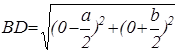Поэтому AD=BD. А так как по определению середины отрезка BC=CD, то теорема доказана.

Можно выбрать систему координат и по-другому (рис.8, рис.9). Если выбрать оси совсем случайно, то легкую задачу можно превратить в очень трудную. Чтобы начать доказательство исходя из рисунка 10, нужно найти способ, позволяющий выразить алгебраически, что треугольник ABC имеет при вершине А прямой угол. Сделать это можно, но будет это не очень просто.

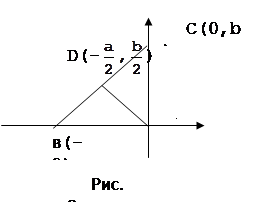
Поэтому необходимо вырабатывать у учащихся, начиная с 6 класса, представления о возможности произвольного выбора системы координат. Эту работу целесообразно вести в процессе решения задач. В целях пропедевтической работы можно рекомендовать в 6 классе задачи из учебника на нахождение координат точек по рисунку, разнообразя их с помощью изменения направления осей и начала координат. (см. приложение1)

Новое в образовании:

Процесс разработки цифровых образовательных ресурсов
Традиционно при описании процедур педагогического дизайна их упорядочивали в виде линейной последовательности (см. Рис. 1). Это описание входит в противоречие с практикой разработки учебных материалов, где неизбежны постоянные циклы: Анализ Разработка Проверка Оценка Анализ Разработка … Рис. 1 Клас ...

Возможности внеурочной деятельности ознакомления с окружающим миром для развития теоретического мышления младших школьников
Экскурсии - один из видов занятий и основная форма организации работы по экологическому воспитанию, одна из трудоёмких и сложных форм обучения. Проводятся экскурсии вне дошкольного учреждения. Это своего рода занятия под открытым небом. Преимущество экскурсий в том, что они позволяют в естественной ...

Современное рабочее место преподавателя на примере кабинета физики
Пример организации рабочего места преподавателя физики в современной школе - полный комплекс ТСО - это качественно новая модель совокупности средств информационных технологий учебного назначения, сочетающих в себе воедино демонстрационные средства, средства индивидуальной работы учащихся и техничес ...