Методические основы обучения координатному методу

Для проведения факультатива предлагается ряд более сложных нестандартных задач, при решении которых используется метод координат.

Задача 1. Два предприятия А и В производят продукцию с одной и той же ценой m за одно изделие. Однако автопарк, обслуживающий предприятие А, оснащен более современными и более мощными грузовыми автомобилями. В результате транспортные расходы на перевозку одного изделия составляют для предприятия А 10 р. на 1 км, а для предприятия В 20 р. на 1 км. Расстояние между предприятиями 300 км. Как территориально должен быть расположен рынок сбыта между двумя предприятиями для того, чтобы расходы потребителей при покупке изделий были минимальными.

Решение:

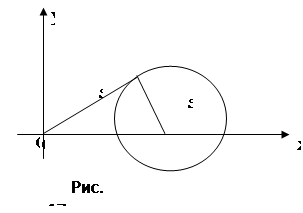Для решения данной задачи воспользуемся методом координат. Систему координат выберем так, чтобы ось Ох проходила через пункты А и В, а ось Оу через точку А. Пусть Р произвольная точка, s1 и s2 расстояния от точки до предприятий А и В (рис.17). Тогда А(0, 0), В(300, 0), Р(х, у).

При доставке груза из пункта А расходы равны m+10s1. При доставке груза из пункта В расходы равны m+20s2. Если для пункта Р выгоднее доставлять груз с предприятия А, то m+10s1< m+20s2, откуда s1<2s2, в обратном случае получим s1>2s2.

Таким образом, границей области для каждой точки, до которой расходы на перевозку груза из пунктов А и В равны, будет множество точек плоскости, удовлетворяющих уравнению

s1=2s2 (1)

Выразим s1 и 2s2 через координаты:

, .

Имея в виду (1), получим .

Это и есть уравнение окружности. Следовательно, для всех пунктов, попадающих во внутреннюю область круга, выгоднее привозить груз из пункта В, а для всех пунктов, попадающих во внешнюю часть круга, - из пункта А.

Задача 2. На плоскости даны точки А и В; найти геометрическое место точек М, удаленных от А в двое больше, чем от В.

Решение:

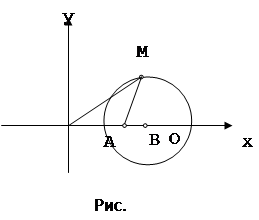Выберем систему координат на плоскости так, чтобы начало координат попало в точку А, а положительная полуось абсцисс пошла по АВ. За единицу масштаба возьмем отрезок АВ. Точка А будет иметь координаты (0,0), точка В координаты (1,0). Координаты точки М обозначим через (х,у). Условие записывается в координатах так:

.

Мы получили уравнение искомого геометрического места точек. Чтобы понять, какое множество описывается этим уравнением, мы преобразуем его так, чтобы оно приняло знакомый нам вид. Возведя обе засти в квадрат, раскрывая скобки и приводя подобные члены, получаем равенство: Зх2-8х+4+Зу2=0.

Это равенство можно переписать так:

или так: . Это уравнение окружности с центром в точке (,0) и радиусом, равным . Это значит, что наше геометрическое место точек является окружностью.

Задача 3.Дан треугольник ABC; найти центр окружности, описанной около этого треугольника.

Решение:

Примем точку А за начало координат, ось абсцисс направим от А к В. Тогда точка В будет иметь координаты (с,0), где с - длинна отрезка АВ. Пусть точка С имеет координаты (q,h), а центр искомой окружности - (а,b). Радиус этой окружности обозначим через R. Запишем в координатах принадлежность точек А(0,0), В(с,0) и C(q,h) искомой окружности:

a2+b2=R2,

(c-a)2+b2=R2,

(q-a)2+(h-b)2=R2.

Каждое из этих условий выражает тот факт, что расстояние точек А(0,0), В(с,0), C(q,h) от центра окружности (а,b) равно радиусу. Эти условия легко получить, если записать уравнение искомой окружности (окружности с центром (а,b) и радиусом R), т. е. (x-a)2+(y-b)2=R2, а затем в это уравнение вместо х и у подставить координаты точек А, В и С, лежащих на этой окружности. Эта система трех уравнений с тремя неизвестными легко решается, и мы получаем:

, ,

.

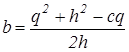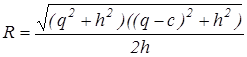Новое в образовании:

Возможности осуществления внеклассной краеведческой работы в специальной школе VII вида
Решая образовательно-воспитательные задачи краеведческого образования в специальной школе VII вида, необходимо учитывать особенности детей с ЗПР и коррекционную направленность всего учебно-воспитательного процесса. На внеклассных занятиях по краеведению коррекционно-развивающие задачи определяются ...

Разработка урока "Развитие проблематики в сочинениях А.П.Чехова"
Антон Павлович Чехов — русский писатель, прозаик, драматург. Родился 17(29) января 1860 года в г. Таганроге. Умер 2(15) июля 1904 года в г. Баденвейлер, Германия; похоронен в Москве, на Новодевичьем кладбище. Антон учился в греческой школе, затем в классической гимназии. Одним из семейных домашних ...

Современное состояние эволюционного учения в школьном курсе биологии
Мир, а вместе с ним и мы, стремительно изменяется. Поток информации из самых разных источников просто захлестывает. Но приходишь в школу – попадаешь в информационный штиль: ни бурь, ни штормов. 20 век подарил биологии несколько важнейших для понимания эволюции инструментов – генетику, учение о биос ...