Анализ учебников

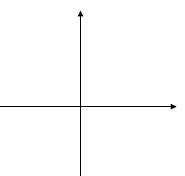
На рисунке 3 графики функций у= 2х², у= х², у= х² изображены в одной системе координат. Мы видим, что чем больше коэффициент а, тем больше «крутизна» параболы. Разная « крутизна» графиков говорит о том, что быстрее всего меняется функция у= 2х², а медленнее всего – функция у= х².

Авторы не объясняют, почему это так происходит, не проводя анализ графиков функций и не вводятся понятия растяжение (сжатие) вдоль оси Оу.

Симметрия относительно оси Ох.

Это понятие вводится на примере графиков функций: у= х² и у= -х².

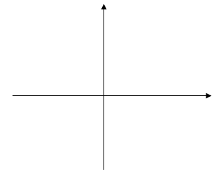
Чтобы получить из графика функции у= х² график функции у= -х², нужно каждую точку первого графика заменить точкой с той же абсциссой, но с противоположной ординатой, т.е. точкой, симметричной точке первого графика относительно оси х. Т. е., эти графики симметричны относительно оси х.

Таким образом, графиком функции у=ах², а≠0, является парабола с вершиной в начале координат; ее осью симметрии является ось у; при а>0 ветви параболы направлены вверх; при а<0 ветви направлены вниз.

Система упражнений в этом учебнике разбита на 2 уровня:

А- обязательные упражнения рассчитанные на «среднего ученика»;

Б- повышенный уровень сложности рассчитанный на более сильных учеников.

В этом блоке авторы предлагают «задачу- исследование». В конце каждой главы задания для самопроверки. Рассмотрим упражнения, которые авторы предлагают для усвоения этих преобразований в группе А:

а) постройте график функции f(x)= х² .

б) постройте в той же системе координат график функции g(х)= -х².

в) вычислите значение выражения f(10). Чему равно значение выражения g(10)?

г) график, какой из функций у= f(x) и у= g(х) пересекает прямую у=100; у=-400? Укажите координаты точек пересечения?

на рисунке изображены графики квадратичных функций, заданных формулами: у= 3,2х²; у= -0,6х²; у= 1,6х²; у= -2х²; у= -х²; у= х². соотнесите каждый из них с одной из формул.

изобразите в одной и той же системе координат схематически графики функций:

у= 0,3х²; у= -10х²; у= 8х²; у= -0,1х².

а) какая парабола самая «крутая»? самая «пологая»?

б) какие из функций имеют наименьшее значение? Наибольшее значение?

в) укажите промежуток убывания и промежуток возрастания функции у= 8х²; у=-0,1х².

в одной системе координат постройте графики функций и найдите координаты их точек пересечения:

Новое в образовании:

Обучение в интернате
Практика обучения этих детей с ДЦП в массовой школе показала, что особенности психического и физического развития не позволяют им полноценно овладевать программой массовой общеобразовательной школы. Обучение детей с нарушениями опорно-двигательного аппарата проводится в специальном типе школ – школ ...

Основные направления педагогико-воспитательной работы с осужденными
Существуют следующие основные направления воспитательной работы в пенитенциарных учреждениях: 1. Правовое воспитание осужденных. Это процесс формирования правосознания, включающего знание принципов и норм права и убеждение в необходимости следовать им. Его задача заключается в том, чтобы максимальн ...

Система коррекционно-педагогической работы
Тесная взаимосвязь развития речи, сенсорных функций, моторики и интеллекта определяет необходимость коррекции нарушений речи при дизартрии у детей с сочетанием со стимуляцией развития всех её сторон, сенсорных и психических функций, осуществляя тем самым формирование речи как целостной психической ...