Анализ учебников

Отметим точки (0;0); (1;-1); (-1;-1); (2;-4); (-2;-4); (-3;-9); (3;-9) на координатной плоскости.

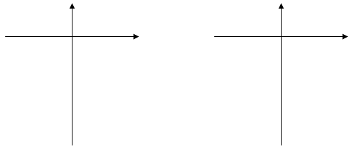
Это парабола с вершиной в точке (0;0), ось у – ось симметрии, но в отличие от случая, когда к>0, на этот раз ветви параболы направлены вниз. Аналогично обстоит дело и для других отрицательных значений коэффициента к.

Если построить в одной системе координат графики функций у= х² и у= -х², то нетрудно заметить, что эти параболы симметричны друг другу относительно оси х.

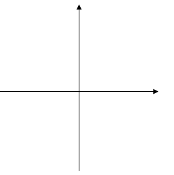
Точно так же симметричны друг другу относительно оси х параболы у=2х²и у=-2х² (постройте эти две параболы в одной системе координат и убедитесь в справедливости сделанного утверждения).

Вообще, график функции у=-f(x) симметричен графику функции у=f(x) относительно оси абсцисс.

II. 1. Параллельный перенос вдоль оси абсцисс.

Это преобразование вводится через сравнение графиков функций у=х² и у=(х+3)².

Графиком функции у=х² является парабола. Для функции у=(х+3)² составим таблицу значений:

Построив график по точкам (-3;0); (-2;1); (-4;1); (-5;4); (-1;4); (-6;9); (0;9), получим параболу. Обратите внимание – это точно такая же парабола, как и у= х², но только сдвинутая вдоль оси х на 3 единицы масштаба влево. Вершина параболы находится в точке (-3;0), а не в точке (0;0), как для параболы у= х². Осью симметрии служит прямая х=-3, а не х=0, как это было в случае параболы у= х².

Если построить в одной системе координат графики функций у= х² и у= (х-2)², заметим, что второй график получается из первого сдвигом (параллельным переносом) вдоль оси х на 2 единицы масштаба вправо.

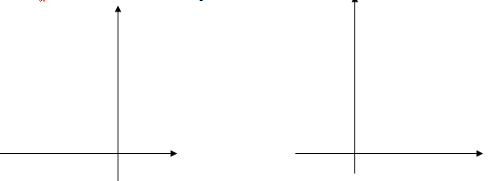
& Вообще, справедливо следующее утверждение:

чтобы построить график функции у=f(x+l),где l- заданное положительное число, нужно сдвинуть график функции у=f(x) вдоль оси х на l единиц масштаба влево;

чтобы построить график функции у=f(x-l),где l- заданное положительное число, нужно сдвинуть график функции у=f(x) вдоль оси х на l единиц масштаба вправо.

Данное преобразование рассматривается не только на примере параболы, но и на гиперболе у= -.

построим гиперболу у= -;

сдвинем ее вдоль оси х на 5 единиц влево.

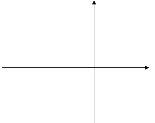
Параллельный перенос вдоль оси ординат.

Данное преобразование рассматривается в такой же последовательности, что и предыдущие преобразования.

Новое в образовании:

Значение театральных занятий в развитии школьников на примере театра-студии «Шанс» Полянской школы-интерната
Театр – магическое слово. Сколько ещё более манящих слов, имеющих отношение к этому искусству: кулисы, сцена, рампа, и, наконец, премьера… Очень часто многие из ребят, которые приходят в студию, смутно представляют себе, чем они будут заниматься. Их представление о театральной деятельности заключае ...

Описание исходного уровня сформированности валеологической грамотности младших школьников
Первым этапом нашего исследование стало исследование уровня сформированности у детей младшего школьного возраста (9 – 10 лет) положительного отношения к здоровью и самого понимания этого феномена как содержания валеологической грамотности. Первым этапом данного исследования являлось проведение заня ...

Воспитательная система в начальной школе как педагогическое явление и понятие
В последние годы в педагогической среде значительно возрос интерес к использованию системного подхода в обучении и воспитании школьников, в управлении жизнедеятельностью образовательного учреждения. В тех учреждениях образования, где построена и успешно функционирует воспитательная система учебного ...