Анализ учебников

у= х² и у= х+1; 3) у= 2х² и у= -2х+4;

у= -0,5х² и у= ; 4) у= -2х² и у= -.

постройте график функции:

у= х, если х ≤0 у= -2х², если х<0

-х² , если х>0 2х² , если х≥0.

Для каждой функции укажите промежуток убывания и промежуток возрастания.

Задания из группы Б.

известно, что график квадратичной функции, заданной формулой вида у= ах², проходит через точку С(-6;-9).

а)укажите координаты точки графика, которая симметрична точке С;

б) найдите коэффициент а;

в) укажите координаты каких-нибудь двух точек, одна из которых принадлежит графику, а другая –нет.

постройте график функции:

у= -х , если х ≤1 у= х+3, если х≤0

х² , если х>1 3х² , если х>0.

- в одной системе координат постройте графики функций:

а)у= |х| и у= -|х|; в) у= х³ и у= -х³;

б)у= и у= -; г) у= и у= -.

на рисунке изображен график функции у= f(x). Перечертите график в тетрадь и в той же системе координат постройте график функции у= -f(x).

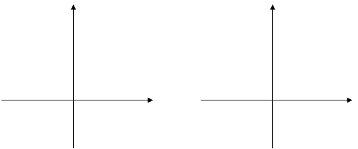
III. При изучении движения графика функции у= ах² вдоль осей координат авторы ставят перед учащимися проблему: Каким уравнением можно задать функцию, график которой получается в результате движения графика функции у=х² вдоль оси у вверх на 2 единицы?

Легко видеть, что абсцисса каждой его точки осталась прежней, а ордината увеличилась на 2. Это значит, что у новой параболы точка с абсциссой х имеет ординату, равную х²+2, т.е. новая парабола является графиком функции у= х²+2.

Аналогично получаем из у= 1,5х² параболу у= 1,5х²-6.

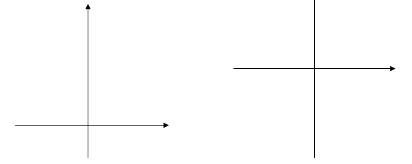
В каждом случае приходим к уравнению вида у= ах²+q, q- ордината вершины новой параболы.

Чтобы построить график функции у= ах²+q, нужно перенести параболу у= ах² вдоль оси у на q единиц вверх, если q>0, или на IqI единиц вниз, если q<0. При этом вершина параболы окажется в точке (0; q).

Обратим внимание, что авторы используют термин – “параллельный перенос”.

IV. Аналогичная проблемная ситуация ставится перед учащимися при движении графика функции у= ах² вдоль оси абсцисс.

В результате решения этой проблемы авторы подводят учащихся к следующим выводам:

- в каждом случае приходим к уравнению вида у= а(х+р)²;

- чтобы построить график функции у= а(х+р)², нужно перенести параболу у= ах² вдоль оси х на р единиц влево, если р>0, или на IрI единиц вправо, если р<0. При этом вершина параболы окажется в точке (-р;0).

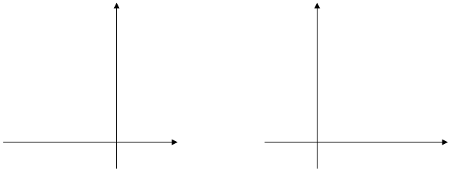
V. Композиция параллельных переносов.

Используя сдвиги параболы вдоль осей координат, можно строить и более сложные графики.

Новое в образовании:

Опыт учителей по использованию дидактических игр как средства активизации познавательной деятельности учащихся
Использование дидактических игр рассмотрим на примере уроков, проводимых в средней школе г. Амурска. В этой школе работает много грамотных, квалифицированных и талантливых учителей, уроки которых дети посещают с большим удовольствием. Одним из учителей в этой школе работает Русанович Любовь Михайло ...

Методы диагностики нарушений звукопроизношения при дизартрии
Особенностью дизартрии у детей является чаще всего ее смешанный характер (сочетание различных клинических синдромов). Наряду с нарушением звукопроизношения проявляются другие речевые расстройства (задержка речевого развития, общее недоразвитие речи, моторная алалия, заикание). Кроме того, страдает ...

Стили педагогического общения и руководства
Особенность профессии учителя состоит в том, что ему необходимы знания, навыки, умения, которые лежат в основе успешного взаимодействия с людьми: организовывать свои отношения с учениками, с коллегами, помогать в нормализации отношений одноклассников между собой, в развитии навыков общения и т.д. Н ...