Анализ учебников

Построим в одной системе координат графики функций: у= х² и у= х²+4.

у= х²+4 точно такая же парабола, как и у= х², но только сдвинутая вдоль оси у на 4 единицы масштаба вверх.

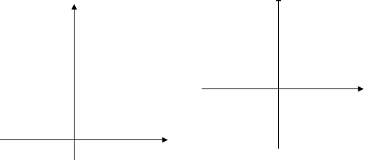
Построим в одной системе координат графики функций: у= х² и у= х²-2

у= х²-2 получается из параболы у= х² сдвигом вдоль оси у на 2 единицы масштаба вниз.

На основе этих примеров выводится правило:

& чтобы построить график функции у=f(x)+m, где m- заданное положительное число, нужно сдвинуть график функции у=f(x) вдоль оси у на m единиц масштаба вверх;

чтобы построить график функции у=f(x)-m, где m- заданное положительное число, нужно сдвинуть график функции у=f(x) вдоль оси у на m единиц масштаба вниз.

Знакомство восьмиклассников с преобразованиями графиков функций заканчивается изучением композицией изученных преобразований.

Рассмотрим следующие примеры:

Построить график функции у= (х-2)²-3.

Осуществим построение по этапам:

Построим график функции у= х²;

Сдвинем параболу у= х² на 2 единицы вправо, получим график функции у=(х-2)²;

Сдвинем параболу у= (х-2)² на 3 единицы вниз, получим график функции у= (х-2)²-3.

Но возможен и другой способ построения:

- графиком функции у= (х-2)²-3 является та же парабола, что и у= х², только вершина переместилась из точки (0;0) в точку (2;-3). Поэтому можем перейти к новой системе координат с началом в точке (2;-3). Для этого построим прямые х=2, у=-3 и воспользуемся шаблоном параболы у= х².

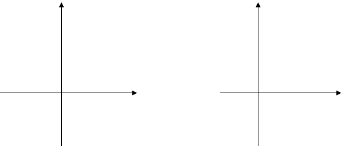
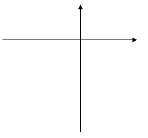
Рассмотрим пример у= -2(х+3)²+1, используя новую систему координат.

Перейдем к вспомогательной системе координат с началом в точке (-3;1);

Привяжем функцию у= -2х² к новой системе координат.

На основе этих примеров авторы предлагают следующие алгоритмы построения графиков функции у=f(x+l)+m.

Алгоритм 1.

Построить график функции у=f(x).

2) Осуществить параллельный перенос графика у=f(x) вдоль оси х на IlI единиц масштаба влево, l>0, и вправо, если l<0;

Осуществить параллельный перенос полученного на втором шаге графика вдоль оси у на ImI единиц масштаба вверх, m>0, и вниз, если m<0.

Алгоритм 2.

Перейти к вспомогательной системе координат, проведя (пунктиром) вспомогательные прямые х=-l, у=m, т.е. выбрав в качестве начала новой системы координат точку (-l; m);

К новой системе координат привязать график функции у=f(x).

Рассмотрим систему упражнений, которая вынесена в отдельную книгу «Задачник». Авторы дают объемный и разноплановый набор упражнений, которого достаточно для работы с учащимися на уроке, для домашних заданий, самостоятельных работ.

В каждом параграфе упражнения сосредоточены по отдельным подтемам, соответствующим теоретическому материалу учебника, внутри подтем достаточно четко выдерживается линия нарастания трудности, что позволяет осуществить дифференцированный подход к обучению.

В каждом параграфе упражнения сконцентрированы по двум блокам:

первый – до черты - содержит задания базового и среднего уровней трудности;

Новое в образовании:

Методические рекомендации и план работы в повседневной жизни по оптимизации двигательной активности детей с задержкой психического развития
С целью оптимизации двигательной активности в детском саду, для детей с ЗПР необходимо создание специальных педагогических условий, предполагающих индивидуально-дифференцированный подход к формированию двигательных навыков и применение комплекса коррекционно-профилактических мероприятий, включающих ...

Эмпирическое исследование формирования коммуникативных универсальных учебных действий
Целью исследования являются формирование коммуникативных универсальных учебных действий. Для достижения цели, поставлены следующие эмпирические задачи: Определить уровень сформированности коммуникативных универсальных учебных действий в начале и в конце учебного года у обучающихся первых классов, с ...

Общие правила организации групповой работы на уроке
Групповая работа учащихся давно вошла в школьную жизнь. Каковы же дидактические условия, с учетом которых должна строиться эта форма обучения? Эти условия описаны в работах эстонского ученого Х.И. Лийметса «Групповая работа на уроке», И.М. Чередова «Система форм организации обучения в общеобразоват ...