Анализ учебников

Построим график функции у= 2(х+1)²-3.

построим параболу у= 2х²;

перенесем ее на 1 единицу влево – получим график функции у= 2(х+1)²;

сдвинем этот график на 3 единицы вниз, получим график функции у= 2(х+1)²-3.

Последовательность построения можно записать в виде схемы:

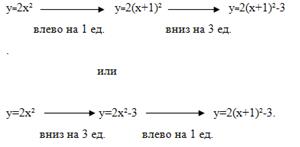
При формулировки следующего правила, авторы используют термин «параллельный перенос».

График функции, заданной формулой вида у= а(х+р)²+q, можно получить из параболы у=ах² с помощью двух параллельных переносов:

- вдоль оси х на IрI единиц – влево или вправо в зависимости от знака числа р;

- вдоль оси у на IqI единиц - вверх или вниз в зависимости от знака числа q.

Вершиной параболы у= а(х+р)²+q будет точка (-р;q).

Система упражнений разнообразна как в уровне А, так и в уровне Б, отражает теоретический материал в следующих заданиях:

задайте функцию формулой и схематически изобразите график функции, если известно, что ее график получен сдвигом вдоль оси у:

а) параболы у= 2х² на 4 единицы вверх;

б) параболы у=х² на 5 единиц вниз;

задайте формулой параболу, изображенную на рисунке, если известно, что она получена сдвигом вдоль оси у параболы:

а) у= х²; б) у= х²; в) у= -2х²; г) у= -х².

постройте график функции:

а) у= х²-1; в) у= х²-2; д) у= (х+2)²+1; ж) у= х²-2х+3;

б) у= -х²+9; г) у= -х²+8; е) у= (х-4)²+1; з) у= х²+6х+8.

изобразите схематически график функции и задайте эту функцию формулой, если известно, что ее график получен сдвигом вдоль оси х:

а) параболы у= 2х² на 3 единицы влево;

б) параболы у= х² на 6 единиц вправо.

При построении графика функции у= ах² +вх+с авторы предлагают учащимся на выбор два способа:

построение с использованием изученных преобразований;

построение с помощью вычисления координаты вершины параболы по формулам и нахождения дополнительных точек.

Мы видим, что теоретический материал изложен в достаточно понятной форме, с учетом возрастных особенностей учащихся, подробно рассмотрены примеры, большая и разнообразная практическая база.

«Алгебра» автор А.Г. Мордкович

Данный учебно-методический комплект состоит из следующих составляющих:

учебника;

задачника;

рабочей тетради;

сборника контрольных работ;

сборника тестов;

методических рекомендаций учителю.

Этот учебный комплект продолжает единую содержательную линию обучения по учебнику «Математика 5-6» Зубарева И.И., Мордкович А.Г.

Данный комплект рекомендован (допущен) Министерством образования РФ к использованию в образовательном процессе в общеобразовательных учреждениях на 2004/05 учебный год.

Новое в образовании:

Понятие « краеведение». Его сущность и значение
Понятие « краеведение» означает всестороннее изучение определенной части страны, города, деревни, улицы, поселения местным населением, для которого эта территория считается родным краем. В разное время в понятие « краеведение» вносилось различное содержание. В 20-х годах ХХ в. оно рассматривалось к ...

Развитие взаимодействия дошкольников со сверстниками в условиях образовательного процесса
Дошкольники в условиях дошкольного учреждения взаимодействуют в разных видах деятельности: в игре, на занятиях, в быту и труде. Сюжетно-ролевая игра играет ведущую роль в формировании положительных взаимоотношений детей и формировании положительных морально-нравственных качеств личности старшего до ...

Методы педагогического стимулирования: требование, перспектива, поощрение, наказание и общественное мнение
Методам воспитания сопутствует педагогическая техника. Она включает в себя искусство общения с воспитанниками, управление их поведением, действиями и поступками, посредством мимики и жестов, выразительной речи, приемов театральной педагогики. Социально-психологическое обеспечение воспитательной дея ...