Система упражнений

г) на единицы вправо и единицы вниз вдоль оси у.

№5. Напишите уравнение параболы у= ах²+ m, график которой изображен:

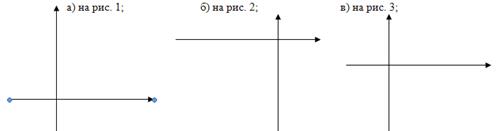
№6. Напишите уравнение гиперболы у= +m, график которой изображен:

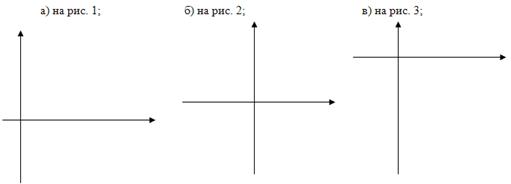
№7. Напишите уравнение функции у= а +m, график которой изображен:

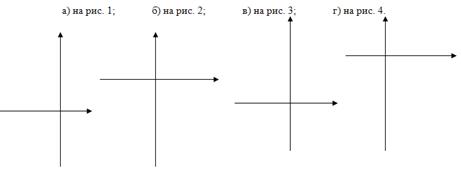
№8. На рисунке построен график функции у= х². Запишите, как построить, и постройте график функции:

1) у= (х-4)²-2; 2) у= (х+3)²+1.

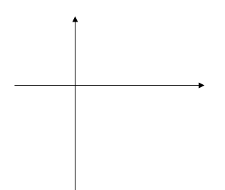
Пример: На рисунке построен график функции у= х². Запишите, как построить, и постройте график функции у= (х-5)²-7.

Решение. Надо установить, вправо или влево, вверх или вниз сдвигать график функции у= х². Чтобы не ошибиться, рассмотрим какую-нибудь точку этого графика, например точку (1;1), и посмотрим, в каком направлении должна переместиться эта точка.

1) Если сравнивать с у= х² график функции у= (х-5)², то значение у=1 здесь достигается не при х=1, а при х-5=1, т.е. при х=6. Это значит, что исходный график сдвигается вправо на 5 единиц.

Если сравнивать графики функций y=f(x), где f(x)= (х-5)², и y=g(x), где g(x)= (х-5)²-7, то при одном и том же значении х=m число g(m) меньше f(m) на 7. Например, если х=3, то f(3)=(3-5)²=4, g(3)=(3-5)²-7= -3.

Точка с координатами (3;1) смещается вниз на 7 единиц.

Следовательно, исходный график у= х² нужно сдвинуть на 5 единиц вправо и на 7 единиц вниз. Постройте график функции у= (х-5)²-7.

№9. Запишите, как построить график функции у=+5.

№10. На рисунке построен график функции у=2,5. Запишите, как построить, и постройте график функции:

1) у= 2,5+2; 2) у= 2,5-3.

Пример: На рисунке построен график функции у=2,5. Запишите, как построить, и постройте график функции у= 2,5+3.

Решение. Надо установить, вправо или влево, вверх или вниз сдвигать график функции у= 2,5. Чтобы не ошибиться, рассмотрим какую-нибудь точку этого графика, например точку (1;2,5), и посмотрим, в каком направлении должна переместиться эта точка.

Если сравнивать с у= 2,5 график функции у= 2,5, то значение у= 2,5 здесь достигается не при х=1, а при =2,5 т.е. при х= 2. Это значит, что исходный график сдвигается вправо на 1 единицу.

Если сравнивать графики функций y=f(x), где f(x)= 2,5, и y=g(x), где g(x)= 2,5+3, то при одном и том же значении х=m число g(m) больше f(m) на 3. Например, если х=5, то f(5)= 2,5=5, g(5)= 2,5+3=8 .

Точка с координатами (5;2,5) смещается вверх на 3 единицы.

Следовательно, исходный график у=2,5 нужно сдвинуть на 1 единиц вправо и на 3 единиц вверх. Постройте график функции у= 2,5+3 .

Новое в образовании:

Методика экспериментального исследования пространственных представлений детей старшего дошкольного возраста с задержкой психического развития
С целью изучения качественного своеобразия и уровня сформированности пространственных представлений у детей с задержкой психического развития, нами было проведено экспериментальное исследование, которое носило сопоставительный характер. В эксперименте участвовали три группы детей, по 10 человек в к ...

Проблемы современной семьи
Свои функции полноценно может выполнять лишь социально благополучная семья. Между тем, в современном обществе наблюдается процесс ослабления семьи как социального института, изменение ее социальных функций, появление неролевых семейных отношений. Семья утрачивает свои ведущие позиции в социализации ...

Реализация кредитно-рейтинговой системы в индивидуально-ориентированном образовательном процессе вуза
Одной из важнейших особенностей вводимых Федеральных образовательных стандартов (ФГОС) является использование зачетных единиц в качестве меры трудоемкости образовательных программ. Показатели трудоемкости образовательных программ в целом, трудоемкости циклов учебных дисциплин заданы в новых стандар ...