Система упражнений

№6. а) (х-3)²-1 > 0; в) х²+3х+2 < 0; д) - ≥ +2;

б) х²+6х+8 ≥ 0; г) -3 ≤ -3х²; е) -3 < -(х+2) ²+1.

3.6 Графики с модулями

№1. Постройте график функции.

Рассмотрим некоторые примеры из этого параграфа.

Пример 1.

у = -5; у = -5; у = -5; у = -5.

Решение:

а) у = -5

1) построим график функции у = ;

2) сдвинем график функции у = на 5 единиц вниз вдоль оси ординат (рис.1).

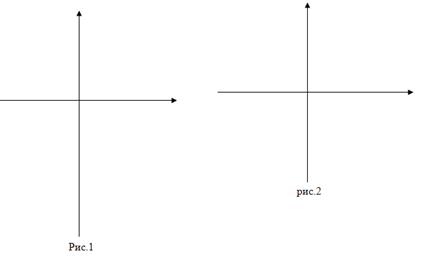
б) у = -5

1) построим график функции у = при х≥0;

2) сдвинем график функции у = ( при х≥0) на 5 единиц вниз вдоль оси ординат;

3) отразим график из п.2 симметрично оси ординат (рис.2).

в) у = -5

1) построим график функции у = ;

2) сдвинем график функции у = на 5 единиц вниз вдоль оси ординат;

3) часть графика, лежащую ниже оси абсцисс, симметрично отразим относительно оси абсцисс (рис.3).

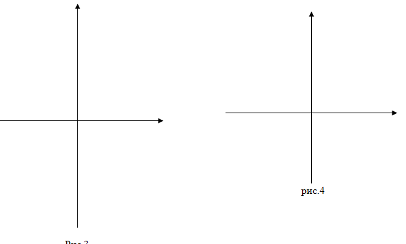
Рис.3

г) у = -5

1) построим график функции у = , при х≥0;

2) сдвинем график функции у = , при х≥0, на 5 единиц вниз вдоль оси ординат;

3) отразим график из п.2 симметрично оси ординат;

4) часть графика из п.3, лежащую ниже оси абсцисс, симметрично отразим относительно оси абсцисс (рис.4).

у = -2; у = -2; у = -2; у = - 2;

у = ; у = ; у = ; у = ;

Новое в образовании:

Планы-конспекты занятий по дисциплине «Конструирование и производство автотракторной техники»
План-конспект занятия на тему «Передний ведущий мост автомобиля» Занятие 1. Дата проведения Тема занятия: Передний ведущий мост автомобиля Цели занятия: Обучающая: Дать понятие о переднем ведущем мосте автомобиля. Воспитательная: Воспитать трудолюбие и самостоятельность. Развивающая: Развитие позна ...

Анализ школьных программ и учебников по русскому языку для начальной школы
Однородные члены предложения в начальной школе по разным системам изучаются в разных классах, так по системе Л.В. Занкова изучение происходит в 3 классе, а по программе М.С. Соловейчик, Н.С. Кузьменко - в 4 классе. В 3 классе по программе А.В. Поляковой изучаются главные и второстепенные члены пред ...

Особенности и роль наглядного обучения в решении образовательно-воспитательных задач
Наглядным называется такое обучение, при котором представления и понятия формируются у учащихся на основе непосредственного восприятия изучаемых явлений или с помощью их изображений. Применяя наглядность, преподаватель вносит в обучение чрезвычайно важный момент - живое созерцание, которое, как изв ...