Анализ учебников

1 случай. Известна функция у=f(x), построить график функции у=mf(x), где m-положительное число.

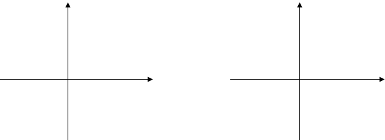
Ординаты точек графика функции у=mf(x) получаются в результате умножения соответствующих ординат точек графика функции у=f(x) на число m. Такое преобразование графика называют – растяжением от оси х с коэффициентом m. Точки пересечения графика функции у=f(x) с осью х остаются на месте.

Если m<1, то используют другой термин – сжатие к оси х с коэффициентом .

у=² и у=² у=х³ и у=0,5х³.

Во 2 случае. Известна функция у=f(x), построить график функции у=-f(x), где m=-1.

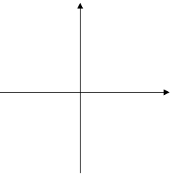
Ординаты отличаются только знаком от функции у=f(x). Точки (х; f(x)) и (х; -f(x)) симметричны относительно оси х. График функции у=-f(x) можно получить из графика функции у=f(x) симметрией относительно оси х.

у= х⁴ и у= -х⁴

В 3 случае. Известна функция у=f(x), построить график функции у=mf(x), где m-отрицательное число.

Авторы вводят равенство mf(x)=-ImIf(x) и порядок построения графика функции у=-ImIf(x) сводится к следующему:

построить график функции у=f(x);

растянуть (сжать) от оси х с коэффициентом ImI;

подвергнуть полученный график симметрии относительно оси х.

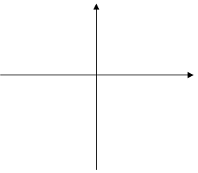
Построим график функции у= -2.

построим график функции у=;

осуществим растяжение графика от оси х с коэффициентом 2, получим график функции у= 2;

подвергнем график функции у= 2 преобразованию симметрии относительно оси х, получим график функции у= -2.

В задачнике приводится следующая система упражнений:

используя график функции у=f(x), где f(x)=, f(x)= х⁻² построить график функции:

а) у= -f(x); б) у= 0,5f(x); в) у= -2f(x); г) у= -3f(x).

постройте график функции:

а) у= х³; б) у= -0,5х³; в) у= -2х³; г) у= 0,5х³.

решите графически уравнение:

а) 2х³ = х+1; б) –0,5х⁴ = 4х; в) 2х⁻⁴ = х+1; г) -3= х-4.

постройте и прочитайте график функции у=f(x):

а) f(x) = 2х ⁻², если х<0; б) -2, если х≤-1

3х³, еслих≥0; f(x) = 2х³, если –1<x≤1

, если x<1.

Задачник “Алгебра – 9 “ содержит раздел “ Домашняя контрольная работа”, которого до этого в задачниках не было.

Мы видим, что материал изложен последовательно, с нарастающей степенью сложности, понятно и доступно для учащихся, с богатой практической системой упражнений.

«Алгебра 7-9» авторы С.М. Никольский, М. К. Потапов

Новое в образовании:

Содержание работы по формированию лексического строя речи у детей с ОНР
На ранних этапах овладения языком ведущая роль принадлежит лексическому уровню, а в дальнейшем на первый план выступает словообразовательный уровень. Овладение словообразованием осуществляется на основе мыслительных операций анализа, сравнения, синтеза, обобщения и предполагает достаточно высокий у ...

Компетентностный подход в обучении информатике на основе кейс-метода
Современная научная картина мира резко отличается от той, которая была сформирована в доиндустриальном обществе. Мир, который окружает нас, в большей степени хаотичен, чем упорядочен, поэтому в нем трудно построить жизнь, опираясь на готовые рецепты, алгоритмы, технологии. По мнению С.А. Бешенкова ...

Анализ современной ситуации в области информатизации образования
Информационные и коммуникационные технологии (ИКТ) занимают особое место в современном мире. Работа на компьютере, умение использовать ИКТ в работе, умение создавать, а главное использовать информационные ресурсы, находящиеся в распоряжении человечества, являются основополагающими приоритетами ново ...