Анализ учебников

Данный учебно-методический комплект является составной частью единой содержательной линией с 5 по 11 класс, которая рекомендована (допущена) Министерством образования РФ к использованию в образовательном процессе в общеобразовательных учреждениях на 2004/05 учебный год.

Материал излагается на высоком теоретическом уровне, например, учащиеся знакомятся с понятием функция в двух интерпретациях по Лобачевскому и по Дирихле.

Для каждой главы авторы предлагают дополнения с геометрическими сведениями и дополнительным материалом, которые могут быть использованы как в общеобразовательных классах, так и в классах с углубленным изучением математики.

По программе в 8 классе учащиеся знакомятся с понятием функция, функциями: у=х; у=х²; у=; у=кх; у=кх+в, а также преобразованиями: параллельным переносом, растяжением (сжатием) вдоль оси Оу, симметрией относительно оси Ох.

В 8 классе учащиеся знакомятся со степенной функцией.

На изучение преобразований графиков функций в планировании в 8 классе отводится 7 часов:

§7. Квадратичная функция.

7.1. Функция у=ах² (а>0). 2 часа

7.2. Функция у=ах² (а>0). 2 часа

7.3. Функция у=а(х-х₀)²+у 3часа

Последовательность рассмотрения преобразований графиков функций такая же, как у Ю.Н.Макарычева, Н.Г. Миндюк.

Растяжение (сжатие) авторы разбирают на примере функций: у= х² и у= 2х²; у= х² и у= х².

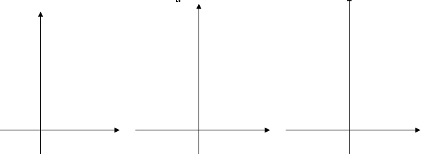
Рассмотрим две функции у= х² и у= 2х². Зададим декартову систему координат хОу и число х₀. Точка А(х;х₀²) принадлежит графику функции у= х², а точка А₁(х;2х₀²), имеющая ту же абсциссу, принадлежит графику функции у= 2х².ординаты точек А₁ и А находятся в отношении 2:1, т.е. отрезок А₀А₁ получается растяжением отрезка А₀А в 2 раза.(рис.1).

График функции у= 2х² получается из графика функции у= х² растяжением последнего в 2 раза вдоль оси Оу.

Рассуждая аналогично, можно показать, что график функции у= ах², если а>1, получается из графика функции у= х² растяжением последнего в а раз вдоль оси у; если же 0<а<1, то сжатием последнего в раз.

Система упражнений достаточно разнообразная, первое преобразование отражено в следующих заданиях:

постройте график функции, выбрав удобный единичный отрезок на координатных осях:

1) у= 4х²; 2) у= 0,25х²; 3) у= х²; 4) у= 1,5х²;

5) у= 20х²; 6) у= 400х²; 7) у= 0,001х²; 8) у= 1000х².

постройте параболу у= 0,1х²:

а) при каких х функция принимает положительные значения?

б) при каких х функция равна 2?

в) какие значения принимает у, если х>0,5?

г) при каких х функция возрастает, убывает?

на рисунке представлены графики функций у= х² и у =ах². Определите а.

Далее авторы знакомят учащихся с:

II Симметрией относительно оси Ох следующим образом.

Новое в образовании:

Опытно-экспериментальная работа по организации групповойработы
На первом этапе (констатирующем) было необходимо установить уровень взаимодействия учащихся в группе, определить роль каждого ученика. Для достижения поставленной цели были использованы следующие методы: наблюдения за учениками при работе в группе; беседа с учащимися. Экспериментальное исследование ...

Проектирование профессиональных компетенций студентов
Система непрерывного профессионального образования призвана обеспечить поступательное развитие личности студента как субъекта целеполагания собственной деятельности, ориентированного на непреходящие ценности. Анализ динамики развития современного профессионального образования показывает, что целью ...

Анализ формирования мышления в традиционном преподавании биологии
В современной школе используется три относительно обособленных и отличающихся рядом признаков вида обучения: Объяснительно-иллюстративное, называемое также традиционным, сообщающим или конвенциональным (обычным); Проблемное; Программированное и развившееся на его основе компьютерное обучение. Педаг ...