Анализ учебников

а) у=х² и у=х²+2; в) у= и у=;

б) у=х² и у=х²-3; г) у= и у=.

график, какой функции получится, если гиперболу у= перенести:

а) на 3 единицы масштаба вверх вдоль оси у;

б) на 8 единицы масштаба вниз вдоль оси у;

в) на 7,9 единицы масштаба вверх вдоль оси у;

г) на единицы масштаба вниз вдоль оси у.

напишите уравнение гиперболы у= +m, график которой изображен:

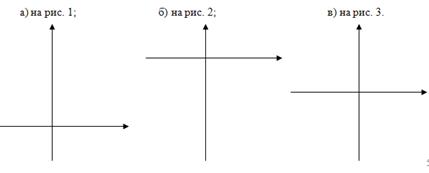
решите графически уравнение:

а) х²+1 = б) -5 = -х

- решите графически систему уравнений:

а) у= 3х²-2 б) у= +1 в) у= -+1

у= 1 у= 3 5х-3у=0.

Композиция преобразований отражена в следующей системе упражнений:

постройте в одной системе координат графики функций:

а) у=х² и у=(х+2)²+1; в) у=2х² и у=2(х-2)²-2

б) у= и у=+3; г) у= и у=-2.

График, какой функции получится, если параболу у= 2,5х² (гиперболу у= -) перенести:

а) на 3 единицы масштаба влево и на 4 единицы вверх;

б) на 1 единицу масштаба вправо и на 5 единиц вниз;

в) на 2 единицы масштаба влево и на 6 единиц вниз;

г) на 1,2 единицы масштаба вправо и на 7 единиц вверх.

постройте график функции:

а) у= (х+1)²-2; в) у= +2;

б) у= -(х+3)²+1; г) у= -+2.

- решите графически систему уравнений:

а) у= -2(х-1)²+5 б) у= -1 в) у= +3

у= 2х+3 у= -3 у= 2х+1.

напишите уравнение параболы у= а(х+l)²+m (гиперболы у= +m) , график которой изображен:

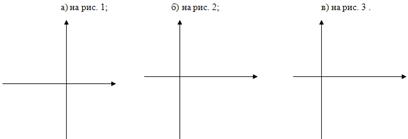
постройте график функции, предварительно преобразовав ее методом выделения полного квадрата к виду у= а(х+l)²+m:

а) у= х²+2х+3; в) у= 2х²-4х+5;

б) у= х²-10х+24; г) у= -3х²+6х-1.

В «Алгебре-9» класса авторы систематизируют все известные свойства функций, учащиеся изучают еще одно преобразование – растяжение (сжатие) относительно осей координат.

Авторы учебника рассматривают три случая преобразования:

Новое в образовании:

Проектирование профессиональных компетенций студентов
Система непрерывного профессионального образования призвана обеспечить поступательное развитие личности студента как субъекта целеполагания собственной деятельности, ориентированного на непреходящие ценности. Анализ динамики развития современного профессионального образования показывает, что целью ...

Коррекционная работа по формированию у детей с задержкой психического развития пространственных представлений
Пространственные функции являются составной частью и предпосылкой многих психических процессов, поэтому коррекционную работу по преодолению различных нарушений при ЗПР целесообразно начинать, прежде всего, с развития у детей элементарных ощущений отдельных свойств предметов и явлений и целостного в ...

Опытно-экспериментальная работа по изучению влияния информационных технологий на развитие количественных представлений у старших дошкольников
Базой исследования является ДОУ № 97 г.Магнитогорска. В эксперименте принимали участие дети старшей группы, в количестве десяти человек. Сроки проведения эксперимента с января по март 2007 года. Исследовательская работа включает в себя констатирующий и формирующий этапы эксперимента. Цель констатир ...